Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Some Applications of Trigonometry

Short Answer Type

161. A pole of height 5 m is fixed on the top of a tower The angle of elevation of the top of the pole as observed from a point A on the ground is 60° and the angle of depression of the point A from the top of the tower is 45°. Find the height of the tower.

95 Views

162. The angles of depression of the top and the bottom of a 9 m high building from the top of a tower are 30° and 60° respectively. Find the height of the tower and the distance between the building and the tower.

124 Views

163. A man on the deck of a ship 14 m above water level, observes that the angle of elevation of the top of a cliff is 60° and the angle of depression of the base of the cliff is 30°. Calculate the distance of the cliff from the ship and the height of the cliff.

259 Views

164. In the following Fig. what are the angles of depression from the observing positions O₁ and O₂ of the object at A?

(a) 30°, 45° (b) 30°, 60° (c) 45°, 60° (d) 45°, 45°

97 Views

165.

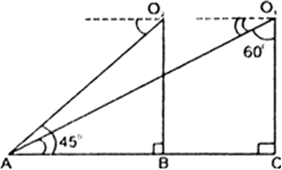
Find the angle of elevation of the sun's altitude when the height of shadow of a vertical pole is equal to its height.
(a) 30° (b) 60° (c) 45° (d) 90°

428 Views

166. The string of a kite is 100 m long and its makes an angle of 60° with the horizontal. Find the height of the kite. Assume that there is no slackness in the string.

(a) 50 m (b) 60 m (c)

50 over 3 space straight m

(d)

50 square root of 3 space straight m space

212 Views

167.

In Fig. 9.74, what are the angles of depressions of the top and bottom of a pole from the top of a tower h m high.
(a) 45°, 70° (b) 45°, 60° (c) 45°, 30° (d) 45°, 45°

161 Views

168. A balloon is connected to a meterological ground station by a cable length 215 m inclined at 60° to the horizontal determine the height of the balloon leave the ground. Assume the there is no slack in the cable.

left parenthesis straight a right parenthesis space space 215 over 2 straight m space space space space space space space space space space left parenthesis straight b right parenthesis space 215 square root of 3 straight m space space space space space space space space space space left parenthesis straight c right parenthesis space fraction numerator 215 square root of 3 over denominator 2 end fraction straight m space space space space space space space left parenthesis straight d right parenthesis space 215 space straight m

99 Views

169.

The angle of elevation of the top of a tower from a point on the grounds which is 30 m away from the foot of the tower is 30°. The height of the tower is

(a) 10 m (b) $fraction numerator 10 over denominator square root of 3 end fraction straight m$ (c) $10 square root of 3 space straight m$ (d) 30 m

105 Views

170.
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.

Let AB be the ladder and CA be the wall.

The ladder makes an angle of 60^o with the horizontal.
∴ ΔABC is a 30^o-60^o-90^o, right triangle.

Given: BC = 2.5 m, ∠ABC = 60°
AB = 5 cm and ∠BAC = 30°

From Pythagoras Theorem, we have
AB² = BC² + CA²
5² = (2.5)² + (CA)²
(CA)² = 25 – 6.25 = 18.75 m
Hence, length of the ladder is $square root of 18.75 end root space almost equal to 4.33 straight m$

4627 Views

Previous Year Papers

Test Series

Test Yourself

Short Answer Type

170. A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.

170.
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder.