 Short Answer Type
Short Answer TypeFind the mode of the distribution from the following data.
|
Class |
Frequcncy |
|
10-15 |
3 |
|
15-20 |
2 |
|
20-25 |
10 |
|
25-30 |
7 |
|
30-35 |
20 |
|
35-40 |
5 |
|
40-45 |
8 |
Determine the value of mode from the following frequency distribution table.
|
Murks (C.I.) |
No. of students (f) |
|
0-10 |
5 |
|
10-20 |
12 |
|
20-30 |
14 |
|
30-40 |
10 |
|
40-50 |
8 |
|
50-60 |
6 |
 Long Answer Type
Long Answer TypeThe marks distribution of 30 students in a mathematics are given in the table. Find the mode of this data. Also compare and interpret the mode and mean.
|
Class interval |
Number of students (f) |
|
10-25 |
2 |
|
25-40 |
3 |
|
40-55 |
7 |
|
55-70 |
6 |
|
70-85 |
6 |
|
85-100 |
6 |
Case I: Finding Mode :
Here, the maximum class frequency is 7 and the class corresponding to frequency is 40 - 55. So the modal class is 40 - 55.
Thuse we have
Model class = 40.55
l = 40
f1 = 7
f0 =3
f2 = 6
and h = 15
Npw substituting these values in the formula of mode, we get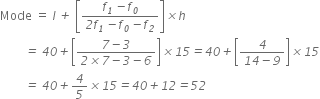
Case II: Finding Mean
|
C.I. |
fi |
xi |
di = x2- 62.5 |
fiui = di/h |
fiui |
|
10-25 |
2 |
17.5 |
- 45 |
- 3 |
- 6 |
|
25-40 |
3 |
32.5 |
- 30 |
- 2 |
- 6 |
|
40-55 |
7 |
47.5 |
- 15 |
- 1 |
- 7 |
|
55-70 |
6 |
62.5 = A |
0 |
0 |
0 |
|
70-85 |
6 |
77.5 |
15 |
1 |
6 |
|
85-100 |
6 |
92.5 |
30 |
2 |
12 |
|
Σfi = 30 |
Σfiui= -1 |
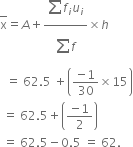
Hence, the mode of the given data is 52 while median is 62.
Interpretation : Maximum number of students obtained 52 marks, while on an average student obtained 62 marks.
 Short Answer Type
Short Answer TypeThe following table shows the marks obtained by 100 students of class X in a school during a particular academic session. Find the mode of this distribution.
|
Marks |
No. of students |
|
Less than 10 |
7 |
|
Less than 20 |
21 |
|
Less than 30 |
34 |
|
Less than 40 |
46 |
|
Less than 50 |
66 |
|
Less than 60 |
77 |
|
Less than 70 |
92 |
|
Less than 80 |
100 |
Calculate the median of the following distribution of incomes of employees of a company.
|
Income |
No. of Persons |
|
400-500 |
25 |
|
500-600 |
69 |
|
600-700 |
107 |
|
700-800 |
170 |
|
800-900 |
201 |
|
900-1000 |
142 |
|
1000-1100 |
64 |
 Long Answer Type
Long Answer TypeFind the mean, mode and median for the following data :
|
Class |
0-10 |
10-20 |
20-30 |
30-40 |
40-50 |
Total |
|
Frequency |
8 |
16 |
36 |
34 |
6 |
100 |
 Short Answer Type
Short Answer TypeThe median of the following data is 52.5. Find the values of x and y if the total frequency is 100.
|
Class Interval |
Frequency |
|
0-10 |
2 |
|
10-20 |
5 |
|
20-30 |
x |
|
30-40 |
12 |
|
40-50 |
17 |
|
50-60 |
20 |
|
60-70 |
y |
|
70-80 |
9 |
|
80-90 |
7 |
|
90-100 |
4 |
|
Total 100 |
Calculate the median from the following data:
|
Value |
Frequency |
|
Less than 10 |
4 |
|
Less than 20 |
16 |
|
Less than 30 |
40 |
|
Less than 40 |
76 |
|
Less than 50 |
96 |
|
Lc9s than 60 |
112 |
|
Less than 70 |
120 |
|
Less than 80 |
125 |
Calculate the median from the following data:
|
Size |
Frequency |
|
More than 50 |
0 |
|
More than 40 |
40 |
|
More than 30 |
98 |
|
More than 20 |
123 |
|
More than 10 |
165 |
 Long Answer Type
Long Answer TypeThe median of the following data is 20.75. Find the missing frequencies x and y, if the total frequency is 100.
|
Class Interval |
0 - 5 |
5 - 10 |
10 - 15 |
15 - 20 |
20 - 25 |
25 - 30 |
30 - 35 |
35 - 40 |
|
Frequency |
7 |
10 |
x |
13 |
y |
10 |
14 |
9 |
