 Long Answer Type
Long Answer TypeA right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose value of π as found appropriate.)
 Short Answer Type
Short Answer TypeA cistern, internally measuring 150 cm × 120 cm × 110 cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm × 7.5 cm × 6.5 cm?
In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km2, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel (see the given Fig.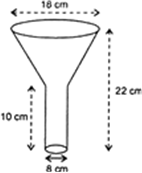
 Long Answer Type
Long Answer TypeDerive the formula for the curved surface area and total surface area of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
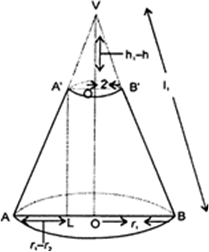
Let h be the height, l the slant height and r1 and r2 the radii of the circular bases of the frustum ABB’ A’ shown in Fig. such that r1 > r2.
Let the height of the cone VAB be h1 and its slant height be i.e., VO = h1 and VA = VB = l1
∴ VA’ = VA – AA’ = l1– l
and VO’ = VO – OO’ = h1– h
Here, ΔVOA ~ ΔVO‘A’
Now,
Height of the cone VA‘B’![]()
Slant height of the cone VA‘B’![]()
Let S denote the curved surface area of the frustum of cone. Then,
S = Lateral (curved) surface area of cone VAB
- Curved surface area of cone VA‘B’
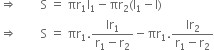
[Using (A) and (C)]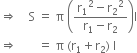
Curved surface area of the frustum
= π(r1 + r2)l
Total surface area of the frustum
= Lateral (curved) surface area
+ Surface area of circular bases
= π (r1 + r2) I + πr12 + πr22
= π {(r1 + r2) l + r12 + r22}.
 Short Answer Type
Short Answer TypeDerive the formula for the volume of the frustum of a cone, given to you in Section 13.5, using the symbols as explained.
