 Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeLet r1 and r2 cm be the radii of the base of the cylinder and cone respectively. Then, r1 = r2 = 8 cm Let h1 and h2 cm be the heights of the cylinder and the cone respectively. Then,
h1 = 240 cm and h2 = 36 cm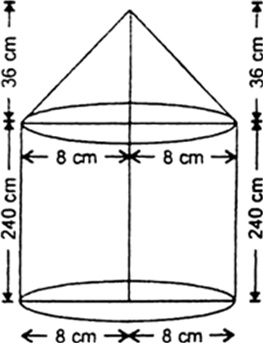
Now, Volume of the cylinder = ![]() r12h1 cm3 = (
r12h1 cm3 = (![]() x 8 x 8 x 240) cm3 = (
x 8 x 8 x 240) cm3 = (![]() x 64 x 240) cm3
x 64 x 240) cm3
Volume of the cone = 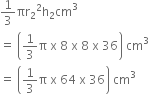
Total volume of the iron = Volume of cylinder + Volume of the cone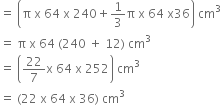
Hence, total weight of the pillar = Volume x Weight per cm3
= (22 x 64 x 36 x 7.5) = 380.16 kg
 Short Answer Type
Short Answer Type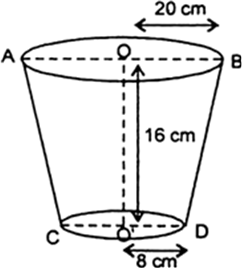
 Long Answer Type
Long Answer Type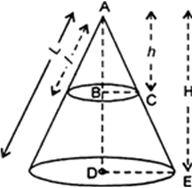
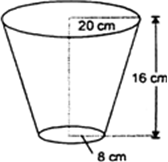
 Short Answer Type
Short Answer TypeA bucket of height 8 cm made up of copper sheets is in the form of frustum of a right circular cone with radii of its lower ends as 3 cm and 9 cm respectively. Calculate
(i) the height of the cone of which the bucket is a part.
(ii) the volume of water which can be filled in the bucket.
(iii) the area of copper sheet required to make the bucket.
