 Long Answer Type
Long Answer Type
Height of the solid metal cylinder, h = 10 cm
Radius of the solid metal cylinder, r = 4.2 cm
therefore,
Radius of each hemisphere = radius of the solid metal cylinder, r = 4.2 cm
Now,
Volume of the rest of the cylinder = Volume of cylinder - 2 x volume of each hemisphere

Thickness of the cylindrical wire = 1.4 cm
Therefore,
Radius of the cylindrical wire, R = 1.4/2 = 0.7 cm
Let the length of the wire be H cm.
It is given that the rest of the cylinder is melted and converted into a cylindrical wire.
therefore,
Volume of the cylindrical wire = Volume of the rest of the cylinder
⇒ π x 0.7 x 0.7 x H = π x (4.2)2 x (4.4)
Hence, the length of the wire is 158.4 cm
 Short Answer Type
Short Answer TypeVolume and surface area of a solid hemisphere are numerically equal. What is the diameter of the hemisphere?
The 3/4th part of a conical vessel of internal radius 5 cm and height 24 cm is full of water. The water is emptied into a cylindrical vessel with internal radius 10 cm. Find the height of water in a cylindrical vessel.
In the given figure, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the shaded region.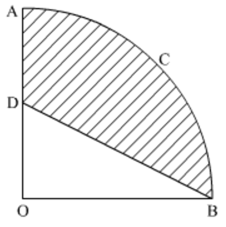
 Long Answer Type
Long Answer TypeIn a hospital used water is collected in a cylindrical tank of diameter 2 m and height 5 m. After recycling, this water is used to irrigate a park of the hospital whose length is 25 m and breadth is 20 m. If the tank is filled completely then what will be the height of standing water used for irrigating the park. Write your views on recycling of water.
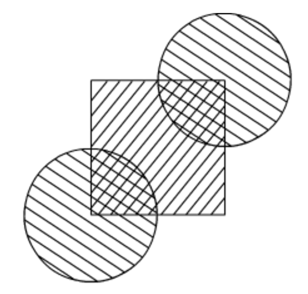
In the given figure, the side of square is 28 cm and radius of each circle is half of the length of the side of the square where O and O' are centres of the circles. Find the area of shaded region.

The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.
 Short Answer Type
Short Answer TypeIf A(–2, 1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram ABCD, find the values of a and b. Hence find the lengths of its sides.
