Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Surface Areas and Volumes

Short Answer Type

741.

The volume of a hemisphere is 2425 $\frac{1}{2}$ cm³^. Find its curved surface area.

$[Use π = \frac{22}{7}]$

Long Answer Type

742.
From a solid cylinder of height 7 cm and base diameter 12 cm, a conical cavity of same height and same base diameter is hollowed out. Find the total surface area of the remaining solid. $[Use π = \frac{22}{7}]$

OR

A cylindrical bucket, 32 cm high and with radius of base 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, then find the radius and slant height of the heap.

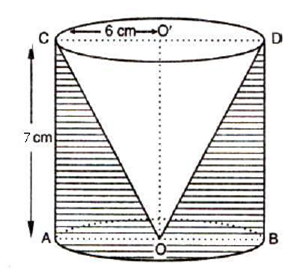
Given: Radius of cylinder = radius of cone = r = 6 cm.

Height of the cylinder = height of the cone = h = 7 cm.

Slant height of the cone = l cm.

$\sqrt{7^{2} + 6^{2}} = \sqrt{85} cm .$

Total surface area of the remaining solid = curved surface area of the

cylinder + area of the base of the cylinder + curved surface area of the cone.

$= (2 πrh + {πr}^{2} + πrl) = 2 x \frac{22}{7} x 6 x 7 + \frac{22}{7} x 6 x 6 + \frac{22}{7} x 6 x \sqrt{85} = 264 + \frac{792}{7} + \frac{132}{7} \sqrt{85} = 264 + 113.14 + \frac{132}{7} \sqrt{85} = 377.14 + \frac{132}{7} \sqrt{85} {cm}^{2}$

Volume if the conical heap = volume of the sand emptied from the bucket.

Volume of the conical heap = $\frac{1}{3} {πr}^{2} h$

= $\frac{1}{3} {πr}^{2} x 24 {cm}^{2}$ .....(Height of the conies 24cm)

...........(1)

Volume of the sand in the bucket = $= {πr}^{2} h = π x {(18)}^{2} x 32 {cm}^{2} . . . . . . . . . (2)$

Equating (1) and (2)

$= \frac{1}{3} {πr}^{2} x 24 = π x (18)^{2} x 32 \Rightarrow r^{2} = \frac{(18)^{2} x 32 x 3}{24} \Rightarrow r^{2} = \frac{18 x 18 x 32 x 3}{24} \Rightarrow r^{2} = 1296 \Rightarrow r = 36 cm$

743.

A bucket is in the form of a frustum of a cone and its can hold 28.49 litres of water. If the radii of its circular ends are 28 cm and 21 cm, find the height of the bucket. $[use π = \frac{22}{7}]$

744.

A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 7 cm and the height of the cone is equal to its diameter. Find the volume of the solid.

$[Use π = \frac{22}{7}]$