 Short Answer Type
Short Answer TypeIf h, c, v are respectively the height, curved surface and the volume of a cone, prove that¬†3ŌÄvh3¬†‚Äď c2h2¬†+ 9v2¬†= 0
Let the base radius and the height of the cone be r and h respectively.
Let the slant height of the cone be l.
Then,
c = ![]() rl 
rl 
¬† ¬† ¬† ¬† ¬† ¬†¬†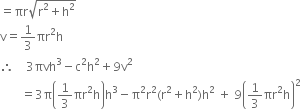
= ŌÄ2r2h2¬†‚Äď ŌÄ2r4h2¬†‚Äď ŌÄ2r4¬†+ ŌÄ2r4h4¬†= 0
A vessel is in the shape of a cone. Radius of the broader end is 2.1 cm and height is 20 cm. Find the volume of the vessel.
A conical tent is to accommodate 11 persons. Each person must have 4 square metre of the space on the ground and 20 cubic metres of air to breath. Find the height of the cone.
