Short Answer TypeFind the length and foot of the perpendicular drawn from the point (3, 4, 5) on the line 
Long Answer TypeShort Answer Type
Long Answer Type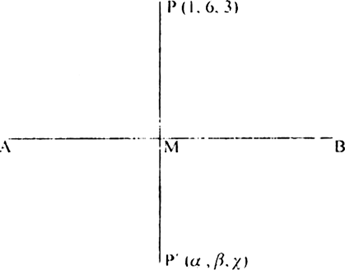
From P (1, 6, 3) , draw PM ⊥ AB and produce it to P' (α, β γ) such that M is mid-point of PP'. Then P' is image of P in line AB.
Any point M as line AB is
(r. 2 r + 1, 3 r + 2)
Direction ratios of AB are 1, 2, 3
Direction ratios of PM are r – 1 , 2 r + 1 – 6 , 3 r + 2 – 3
i.e. r – 1, 2 r – 5, 3 r – 1
∵ PM ⊥ AB∴ (1) (r – 1) + (2) (2 r – 5) + (3) (3 r – 1) = 0
∴ i + 4 r – 10 + 9 r – 3 = 0
∴ 14 r = 14 ⇒ r = 1
∴ M is (1, 3, 5)
Now M is mid-point of PP'
Short Answer Type
Switch
