 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type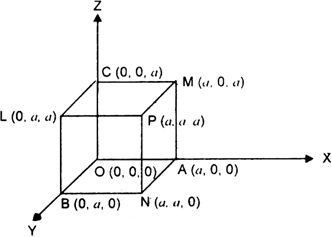
Let OA = OB = OC = a, then the co-ordinates of O , A , B , C are (0, 0, 0), (a, 0, 0), (0, a, 0), (0, 0, a) respectively ; those of P, L, M, N are (a, a, a), (0, a, a), (a, 0, a), (a, a, 0) respectively.
The four diagonals are OP, AL, BM, CN. Direction cosines of OP are proportional to a – 0, a – 0, a – 0, i.e., a, a, a, i.e., 1,1,1.
Direction-cosines of AL are proportional to 0 – a, a – 0, a – 0 i.e., –a, a, a, i.e., – 1, 1, 1.
Direction-cosines of BM are proportional to a – 0, 0 – a, a – 0, i.e., a – a, a i.e., 1, – 1, 1.
Direction-cosines of CN are proportional to a – 0, a – 0, 0 – a i.e., a, a,– a i.e., 1, 1, – 1.![]() direction -cosines of OP are
direction -cosines of OP are ![]()
Directon-cosines of AL are ![]()
Direction-cosines of BM are ![]()
Direction-cosines of CN are ![]()
Let l, m, n be direction-cosines of the line
∴ the line makes an angle α with OP.![]()
![]()
or ![]() ...(1)
...(1)
Similarly ![]() ...(2)
...(2)
![]() ...(3)
...(3)![]()
Squaring and adding (1), (2), (3) and (4), we get,
cos2 α + cos2 β + cos2 γ + cos2 δ
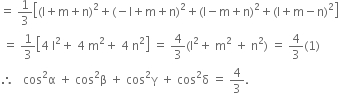
Find the angle between the two lines whose direction cosines are given by the equations:
l + m + n = 0, l2 + m2 – n2 = 0
