Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Long Answer Type

131. Determine whether the following pair of lines intersect:

fraction numerator straight x minus 1 over denominator 2 end fraction space equals fraction numerator straight y plus 1 over denominator 3 end fraction space equals straight z

fraction numerator straight x plus 5 over denominator 5 end fraction space equals space fraction numerator straight y minus 2 over denominator 1 end fraction comma space space straight z space equals space 2

75 Views

Short Answer Type

132. Find the intercepts cut off by the plane x + 2y – 2z = 9 with the axes.

103 Views

133. Find the equation of the plane with intercepts 2, 3 and 4 on the x, y and z-axis respectively.

97 Views

134. Find the intercepts cut off by the plane 2x + y – z = 5.

96 Views

135. Find the intercept form of the equation of the plane x + 3 y – 7 z + 2 = 0.

88 Views

136. Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane..

182 Views

137. Find a unit normal vector to the plane x + 2y + 3z – 6 = 0.

109 Views

138. Find the normal form of the equation of the plane 3x– 4y + z + 5 = 0.

95 Views

139. Find the value of k for which the planes 3 x– 6 y– 2 z = 7 and 2x + y'– k z = 5 are perpendicular to each other.

120 Views

140.
The foot of the perpendicular drawn from the origin to the plane is (4, 3, 2). Find the equation of the plane.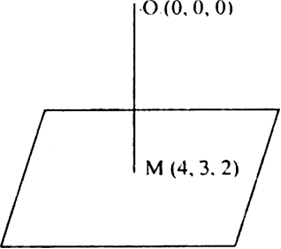

The equation of plane through M (4, 3, 2) is
a (x – 4) + b (Y–3) + c (z – 2) = 0 ...(1)
The direction-ratios of the line through the points O (0, 0. 0) and M (4, 3, 2) are
4 - 0, 3-0, 2-0 i.e. 4, 3, 2
∴ the line OM with direction-ratios 4, 3, 2 is normal to the plane (1)
∴ equation (1) of plane becomes
4 (X – 4) + 3 (y – 3) + 2 (z – 2) = 0 $open square brackets because space space straight a over 4 space equals space straight b over 3 space equals space straight c over 2 close square brackets$
or 4x – 16 + 3 Y – 9 + 2z – 4 = 0 or 4x + 3y + 2z – 29 = 0