 Short Answer Type
Short Answer TypeFind equation of the plane parallel to x + 3y – 2z + 7 = 0 and passing through the origin.
 Long Answer Type
Long Answer TypeThe equation of plane is
2x – 3y + 4z – 6 = 0 ...(1)
Direction ratios of the normal to the plane (1) are 2, –3, 4.
Dividing each by ![]() we get the direction cosines of the normal as
we get the direction cosines of the normal as ![]()
∴ dividing (1) throughout by ![]() we get,
we get, ![]()
This is of the form l x + m y + n z = p, where p is the distance of the plane from the origin.![]() distance of plane from the origin =
distance of plane from the origin = ![]() .
.
Let (x1, y1, z1) be the coordinates of the foot of perpendicular drawn from origin 0(0, 0, 0) to the plane (1).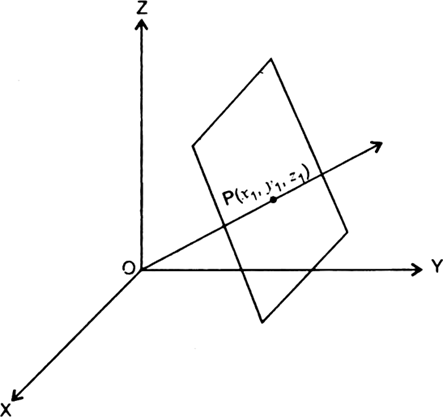
∴ direction ratios of OP are .x1– 0, y, –0, –0 i.e. x1, y1, z1
∴ Direction cosines of OP are![]()
Since direction cosines and direction ratios of a line are proportional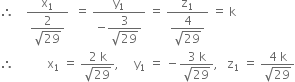
Since P(x1, y1, z1) lies on plane (1)![]()
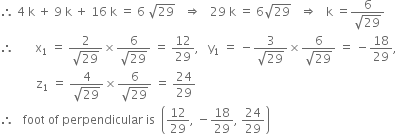
 Short Answer Type
Short Answer TypeIn each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
z = 2
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
x + y + z = 1
