Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Short Answer Type

161.

In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
2x + 3 y – z = 5

94 Views

162.

In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
5y + 8 = 0

91 Views

Long Answer Type

163.

In the following cases, find the coordinates of the foot of the perpendicular
drawn from the origin.
2x + 3y + 4z – 12 = 0

95 Views

164. In the following cases, find the coordinates of the foot of the perpendicular drawn from the origin.
3 y + 4 z – 6 = 0

The equation of plane is
0x + 3 y + 4 z = 6 ...(1)
Dividing both sides by $square root of left parenthesis 0 right parenthesis squared plus left parenthesis 3 right parenthesis squared plus left parenthesis 4 right parenthesis squared end root space equals space square root of 0 plus 9 plus 16 end root space equals space square root of 25 space equals space 5 comma space we space get comma$
$0 straight x plus 3 over 5 straight y plus 4 over 5 straight z space equals space 6 over 5$
It is of form lx + my + nz = p where l = 0, $straight m space equals 3 over 5 comma space straight n space equals space 4 over 5 comma space straight p space equals space 6 over 5$

∴ direction cosines of the normal OP are 0, $3 over 5 comma space 4 over 5$ where O is origin and P (x₁, y₁, z₁) is foot of perpendicular.
Direction ratios of OP are x₁– 0, y₁ – 0, z₁ – 0 i.e. x₁, y₁, z₁.
Since direction cosines and direction ratios of a line are proportional.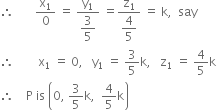
$therefore space space space space space space space straight x subscript 1 over 0 space equals space fraction numerator straight y subscript 1 over denominator begin display style 3 over 5 end style end fraction space equals fraction numerator straight z subscript 1 over denominator begin display style 4 over 5 end style end fraction space equals space straight k comma space space say therefore space space space space space space space space straight x subscript 1 space equals space 0 comma space space space straight y subscript 1 space equals space 3 over 5 straight k comma space space space straight z subscript 1 space equals space 4 over 5 straight k therefore space space space space straight P space is space open parentheses 0 comma space 3 over 5 straight k comma space space 4 over 5 straight k close parentheses$
Since P lies on plane (1)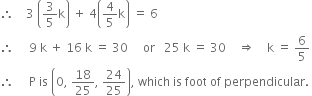
$therefore space space space space 3 space open parentheses 3 over 5 straight k close parentheses space plus space 4 open parentheses 4 over 5 straight k close parentheses space equals space 6 therefore space space space space space 9 space straight k space plus space 16 space straight k space equals space 30 space space space space space or space space space 25 space straight k space equals space 30 space space space space rightwards double arrow space space space space straight k space equals space 6 over 5 therefore space space space space space straight P space is space open parentheses 0 comma space 18 over 25 comma space 24 over 25 close parentheses comma space which space is space foot space of space perpendicular. space$