176.
Find the vector equation of the following planes in scalar product form:
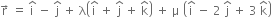
The equation of plane is 
or 
Equating the coefficients of  we get,
we get,
x = 1 + λ + μ ....(1)
y = – 1 + λ – 2 μ ...(2)
z = λ + 3 μ ...(3)
We are to eliminate λ and μ from (1), (2), (3).
Subtracting (2) from (1), we get,
x – y = 2 + 3 μ ... (4)Subtracting (3) from (1), we get,
x – z = 1 – 2 μ ... (5)
Multiplying (4) by 2 and (5) by 3 , we get,
2 x – 2 y = 4 + 6 μ ...(6)
3 x – 3 z = 3 – 6 μ ...(7)
Adding (6) and (7), we get, 5 x – 2 y – 3 z = 7This can be written as 
or

which is the required equation.
74 Views
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type![]()
![]()
 Short Answer Type
Short Answer Type