Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Short Answer Type

171. Find the equation of the plane which is parallel to the x-axis and has intercepts 5 and 7 on the y and z-axis, respectively.

95 Views

172. Find the D.C.’s of the perpendicular from origin to the plane

straight r with rightwards arrow on top. space open parentheses negative 2 space straight i with hat on top space minus space 3 space straight j with hat on top space plus space 6 space straight k with hat on top close parentheses plus 14 space equals space 0.

Find also the distance of the plane from the origin.

77 Views

Long Answer Type

173. A plane meets the coordinate axes in A, B, C and (α, β, γ) is the centroid of the triangle ABC. Then, show that the equation of the plane is

straight x over straight alpha plus straight y over straight beta plus straight z over straight gamma space equals space 3.

82 Views

Short Answer Type

174. A plane meets the co-ordinate axes at A, B, C such that the centroid of the triangle ABC is the point (1, – 2, 3). Show that the equation of the plane is 6x-3y + 2z= 18.

89 Views

Long Answer Type

175. A plane meets the co-ordinate axes at A, B, C such that the centroid of triangle ABC is the point (a, b, c). Show that the equation of the plane is

straight x over straight a plus straight y over straight b plus straight z over straight c equals 3.

91 Views

Short Answer Type

176. Find the vector equation of the following planes in scalar product form:

straight r with rightwards arrow on top space equals space straight i with hat on top space minus space straight j with hat on top space plus space straight lambda open parentheses straight i with hat on top space plus space straight j with hat on top space plus space straight k with hat on top close parentheses space plus space straight mu space open parentheses straight i with hat on top space minus space 2 space straight j with hat on top space plus space 3 space straight k with hat on top close parentheses

74 Views

177. Find the vector equation of the following planes in scalar product form:

straight r with rightwards arrow on top space equals space 2 space straight i with hat on top space minus space straight k with hat on top space plus space straight lambda space straight i with hat on top space plus space straight mu space open parentheses straight i with hat on top space minus space 2 space space straight j with hat on top space minus space straight k with hat on top close parentheses

75 Views

Long Answer Type

178. Find the vector equation of the plane in scalar product form
$straight r with rightwards arrow on top space equals space straight i with hat on top space minus space straight j with hat on top space plus space straight lambda space open parentheses straight i with hat on top space plus space straight j with hat on top space plus space straight k with hat on top close parentheses space plus space straight mu space open parentheses 4 straight i with hat on top space minus space 2 space straight j with hat on top space plus space 3 space straight k with hat on top close parentheses.$

The equation of plane is

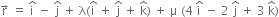
straight r with rightwards arrow on top space equals space straight i with hat on top space minus space straight j with hat on top space plus space straight lambda left parenthesis straight i with hat on top space plus space straight j with hat on top space plus space straight k with hat on top right parenthesis space plus space straight mu space left parenthesis 4 space straight i with hat on top space minus space 2 space straight j with hat on top space plus space 3 space straight k with hat on top right parenthesis

straight x straight i with hat on top space plus space straight y straight j with hat on top space plus space straight z space straight k with hat on top space equals space open parentheses 1 plus straight lambda plus 4 straight mu close parentheses straight i with hat on top space plus space left parenthesis negative 1 plus straight lambda minus 2 straight mu right parenthesis space straight j with hat on top space plus space left parenthesis straight lambda plus 3 straight mu right parenthesis space straight k with hat on top

Equating the coefficients of

straight i with hat on top comma space straight j with hat on top comma space straight k with hat on top comma space space we space get comma

x = 1 + λ + 4 μ    ...(1)
y = – 1 + λ – 2 μ    ...(2)
z = λ + 3 μ    ...(3)
We are to eliminate λ and μ from (1), (2), (3)
Subtracting (2) from (1), we get,
x – y =2 + 6 μ        ...(4)
Subtracting (3) from (1), we get,
x – z = 1 + n    ...(5)
Multiplying (4) by 1, (5) by –6, we get,
x – y = 2 + 6 μ    ...(6)
– 6 x + 6 z = – 6 – 6 μ    .....(7)
Adding (6) and (7), we get,
– 5 x – y + 6 z = – 4
or 5 x + y – 6 z = 4
or

open parentheses straight x straight i with hat on top space plus space straight y space straight j with hat on top space plus space straight z space straight k with hat on top close parentheses. space space open parentheses 5 space straight i with hat on top space plus space straight j with hat on top space minus space 6 space straight k with hat on top close parentheses space equals 4

straight r with rightwards arrow on top. space left parenthesis 5 straight i with hat on top space plus space straight j with hat on top space minus space 6 space straight k with hat on top right parenthesis space equals space 4 comma

which is required vector equation of plane.

73 Views

179.

Find the vector equation in scalar product form of the plane that contains the lines.
$straight r with rightwards arrow on top space equals space left parenthesis straight i with hat on top space plus space straight j with hat on top right parenthesis space plus space straight s space left parenthesis straight i with hat on top space plus 2 space straight j with hat on top space minus space straight k with hat on top right parenthesis$
and $straight r with rightwards arrow on top space equals space open parentheses straight i with hat on top plus straight j with hat on top close parentheses plus straight t open parentheses negative straight i with hat on top space plus space straight j with hat on top space minus space 2 space straight k with hat on top close parentheses$

80 Views

Short Answer Type

180. Find the vector equation of the straight line passing through (1, 2, 3) and perpendicular to the plane

straight r with rightwards arrow on top. space open parentheses straight i with hat on top space plus space 2 space straight j with hat on top space minus space 5 space straight k with hat on top close parentheses space plus space 9 space equals 0 space

89 Views