 Long Answer Type
Long Answer TypeThe equation of plane through the line of intersection of the planes
3x – 4y + 5z – 10 = 0 and 2x + 2y – 3z – 4 = 0 is
(3x – 4 y + 5 z – 10) + k (2x + 2y – 3z – 4) = 0 ...(1)
or (2k + 3) x + (2k – 4) y + (–3 k + 5) z – (4k + 10) = 0
Direction ratios of normal to the plane are
2k + 3, 2k – 4, –3k + 5
Consider the line x = 2y = 3z
or ![]()
or ![]()
Its direction ratios are 1, ![]()
Since this line is parallel to plane (1).
∴ this line is perpendicular to the normal to the plane (1).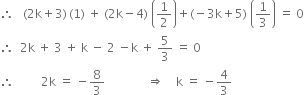
Putting ![]()
![]()
or 3 (3x – 4y + 5z – 10) – 4 (2x + 2 y – 3z – 4) = 0
or 9x – 12y + 15z – 30 – 8x – 8y + 12z + 16 = 0
or x – 20y + 27z = 14
which is required equation of plane.
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type