 Multiple Choice Questions
Multiple Choice QuestionsThe distance of the point (- 2, 4, - 5) from the line is
A.
The line passes through A(- 3, 4, - 8) and is parallel to the vector b =
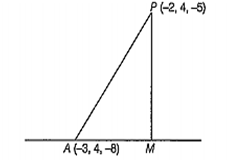
Let M be the foot of the perpendicular from P(- 2, 4, - 5) on the given line.
We, have
Clearly, AM = Projection of AP on b
If the equation of the locus of a point equidistant from the points (a1, b1) and (a2, b2) is (a1 - a2)r + (b1 - b2)y + c = 0, then the value of 'c' is
A tetrahedron has vertices at 0(0, 0, 0), A(1, 2, 1), B(2, 1, 3) and C(- 1, 1, 2). Then, the angle between the faces OAB and ABC will be
