The ratio in which the xy-plane divides the join of (a, b, c) and (- a, - c, - b), is

• a : b

• b : c

• c : a

• c : b

Lines $\frac{\mathrm{x} - 2}{1} = \frac{\mathrm{y} - 3}{1} = \frac{\mathrm{z} - 4}{- \mathrm{k}}$ and $\frac{\mathrm{x} - 1}{\mathrm{k}} = \frac{\mathrm{y} - 4}{2} = \frac{\mathrm{z} - 5}{1}$ will be coplanar, if

• k = 0 or - 1

• k = 1 or - 1

• k = 0 or - 3

• k = 3 or - 3

The equation of the plane containing the line

$\frac{\mathrm{x} - {\mathrm{x}}_1}{\mathrm{l}} = \frac{\mathrm{y} - {\mathrm{y}}_1}{\mathrm{m}} = \frac{\mathrm{z} - {\mathrm{z}}_1}{\mathrm{n}}$ is

a(x - x₁) + b(y - y₁) + c(z - z₁) = 0, where

• ax₁ + by₁ + cz₁ = 0

• al + bm + cn = 0

• $\frac{\mathrm{a}}{\mathrm{l}} + \frac{\mathrm{b}}{\mathrm{m}} + \frac{\mathrm{c}}{\mathrm{n}}$

• lx₁ + my₁ + nz₁ = 0

Distance between the is $\frac{\mathrm{x} - 1}{3} = \frac{\mathrm{y} + 2}{- 2} = \frac{\mathrm{z} - 1}{2}$ and the plane 2x + 2y - z = 6, is

• 9 unit

• 1 unit

• 2 unit

• 3 unit

If (1, 1, 1), (1, - 1, 1), (- 7, - 3, - 5) and (p, 2, 3) are coplanar, then the value of p will be

• 5

• 3

• 2

• None of these

If u, v, ware three non-coplanar vectors, then (u + v - w){(u - v) x (v - w)} is equal to

• $\mathrm{u} . \left(\mathrm{v} \times \mathrm{w}\right)$

• $\mathrm{v} . \left(\mathrm{u} \times \mathrm{w}\right)$

• $\mathrm{w} . \left(\mathrm{u} \times \mathrm{v}\right)$

• 0

If the vectros  $\hat{\mathrm{i}} - 3\hat{\mathrm{j}} + 2\hat{\mathrm{k}}$, $- \hat{\mathrm{i}} + 2\hat{\mathrm{j}}$ represents the diagonals ofa parallelogram, then its area will be

• $\sqrt{21} \mathrm{sq} \mathrm{unit}$

• $\frac{\sqrt{21}}{2} \mathrm{sq} \mathrm{unit}$

• $2\sqrt{21} \mathrm{sq} \mathrm{unit}$

• $\frac{\sqrt{21}}{4} \mathrm{sq} \mathrm{unit}$

If ABCD is a parallelogram. AB = $2\hat{\mathrm{i}} + 4\hat{\mathrm{j}} - 5\hat{\mathrm{k}}$ and AD = $\hat{\mathrm{i}} + 2\hat{\mathrm{j}} + 3\hat{\mathrm{k}}$, then unit vector in the direction of BD is

• $\frac{1}{\sqrt{69}}\left(\hat{\mathrm{i}} + 2\hat{\mathrm{j}} - 8\hat{\mathrm{k}}\right)$

• $\frac{1}{69}\left(\hat{\mathrm{i}} + 2\hat{\mathrm{j}} - 8\hat{\mathrm{k}}\right)$

• $\frac{1}{\sqrt{69}}\left(- \hat{\mathrm{i}} - 2\hat{\mathrm{j}} + 8\hat{\mathrm{k}}\right)$

• $\frac{1}{69}\left(- \hat{\mathrm{i}} - 2\hat{\mathrm{j}} + 8\hat{\mathrm{k}}\right)$

669.

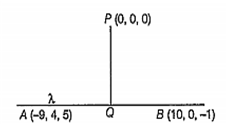
The coordinates of foot of perpendicular drawn from the origin on the line formed by joining the points (- 9, 4, 5)and (10, 0, - 1), are

• (- 3, 2, 1)

• (1, 2, 2)

• (4, 5, 3)

• None of these

If the direction cosines of two lines are represented by l + m + n = 0 and 2lm + 2nl - mn = 0, then the angle between these lines will be

• $\frac{\mathrm{\pi }}{3}$

• $\frac{2\mathrm{\pi }}{3}$

• $\mathrm{\pi }$

• None of these