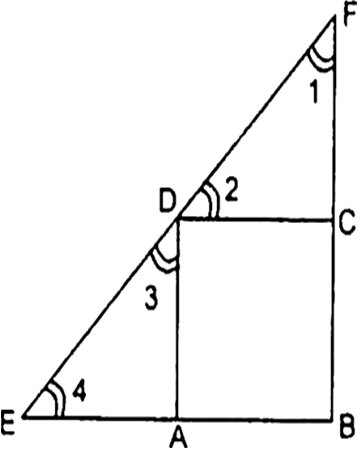
Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeIn the given Fig. DEFG is a square and ∠BAC = 90°. Prove that
(i) ∆AGF ~ ∆DBG.
(ii) ∆AGF ~ ∆EFC.
(iii) ∆DBG ~ ∆AEFC
(iv) DE2 = BD × EC.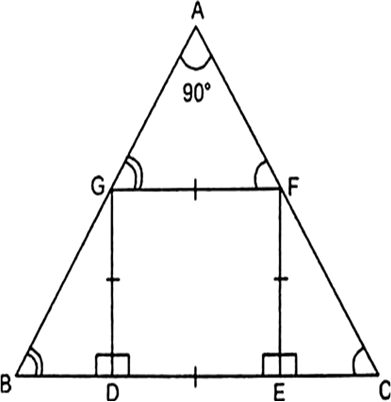
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type