 Long Answer Type
Long Answer TypeState and Prove Converse of Pythagoras Theorem.
Use the above theorem to prove the following:
In a quadrilateral ABCD, ∠B = 90. If AD2= AB2 + BC2 + CD2, prove that ∠ACD = 90°.
The ratio of the areas of similar triangles is equal to the ratio of the squares on the corresponding sides. Prove it.
Using the above theorem, prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described on its diagonals.
In a right-angled triangle, the square of the hypotenuse is equal to the sum of the square on the other two sides. Prove
Using the above theorem, determine the length of AD in terms of b and c.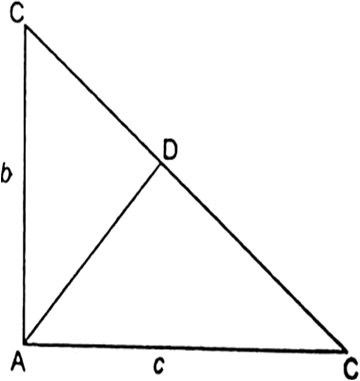
In a right triangle, prove that the square on the hypotenuse is equal to sum of the squares on the other two sides.
Using the above result, prove the following: In the Fig, PQR is a right triangle, right angled at Q. If QS = SR, show that PR2 = 4PS2 - 3PQ2.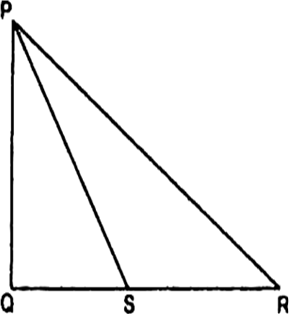
 Short Answer Type
Short Answer Type