Trying to find the right answer to this..

Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

211. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

590 Views

212. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
(A) 2 : 1 (B) 1 : 2 (C) 4 : 1 (D) 1 : 4.

128 Views

213.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3 (b) 4 : 9
(c) 81 : 16 (d) 16 : 81.

We know that the ratio of the areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.
Therefore,
Ratio of the areas of these triangles
= 4² : 9² = 16 : 81
Hence, (d) 16:81 is the correct option.

106 Views

Long Answer Type

214. Sides of some triangles are given below. Determine which of them are right triangles. In case of a right angle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm.

892 Views

215. PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR show that PM² = QM × MR.

283 Views

216.

In the given fig, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB² = BC .BD
(ii) AC² = BC. DC
(iii) AD² = BD . CD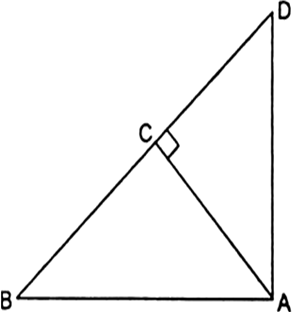

214 Views

Short Answer Type

217. ABC is an isosceles triangle right angled at C. Prove that AB² = 2AC².

233 Views

218. ABC is an isosceles triangle with AC = BC. If AB² = 2AC², prove that ∆ABC is a right triangle.

844 Views

Long Answer Type

219. ABC is an equilateral triangle of side 2a. Find each of its altitudes.

397 Views

220. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

198 Views

Previous Year Papers

Test Series

Test Yourself

Short Answer Type

213. Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio(a) 2 : 3 (b) 4 : 9(c) 81 : 16 (d) 16 : 81.

Long Answer Type

Short Answer Type

Long Answer Type

213.
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3 (b) 4 : 9
(c) 81 : 16 (d) 16 : 81.