Short Answer Type
Short Answer TypeSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3 (b) 4 : 9
(c) 81 : 16 (d) 16 : 81.
 Long Answer Type
Long Answer Type(i) 7 cm, 24 cm, 25 cm
72 = 49
242 = 576
and 252 = 625
We see that
72 + 242 = 252
∴ The given triangle is right angled
Hypotenuse = 25 cm.
(ii) 3 cm, 8 cm, 6 cm
32 = 9
82 = 64
62 = 36
∵ 32 + 62 ≠ 82
∴ The given triangle is not right angled.
(iii) 50 cm, 80 cm, 100 cm
502 = 2500
802 = 6400
1002 = 10000
∵ 502 + 802 ≠ 1002
∴ The given triangle is not right angled.
(iv) 13 cm, 12 cm, 5 cm
132 = 169
122 = 144
52 = 25
∵ 52 + 122 ≠ 132
∴ The given triangle is right angled
Hypotenuse = 13 cm.
In the given fig, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB2 = BC .BD
(ii) AC2 = BC. DC
(iii) AD2 = BD . CD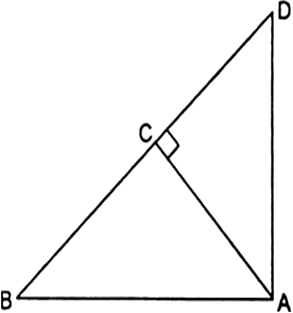
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type