Short Answer Type
Short Answer TypeSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3        (b) 4 : 9
(c) 81 : 16    (d) 16 : 81.
 Long Answer Type
Long Answer TypeIn the given fig, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB2 = BC .BD
(ii) AC2 = BC. DC
(iii) AD2 = BD . CD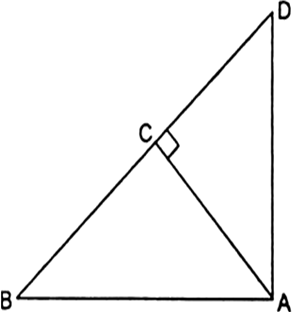
Proof : (i) In ‚ąÜBAC and ‚ąÜBDA,
‚ą†BAC = ‚ą†BDA ¬†¬†¬†...(i)
In right triangle ABC, we have
‚ą†BAC + ‚ą†CBA = 90¬į ¬†¬†¬†...(ii)
In right triangle ABD, we have
‚ą†BDA + ‚ą†CBA = 90¬į ¬†¬†¬†...(iii)
Comparing (ii) and (iii), we get
‚ą†BAC = ‚ą†BDA
And, ¬†¬†¬†‚ą†ACB = ‚ą†DAB
[Each equal to 90¬į]
‚ąī ¬†¬†¬†‚ąÜBAC ~ ‚ąÜBDA
[Using AA similar condition]
‚ąī ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†![]()
[‚ąĶ Corresponding sides of two similar triangles are proportional]
⇒    BA2 = BC . BD
⇒    AB2 = BC . BD.
(ii) In right triangle ACB and DCA,
‚ą†ACB = ‚ą†DCA = 90¬į
‚ą†BAC = ‚ą†ADC
‚ąī ¬†¬†¬†‚ąÜACB ~ ‚ąÜDCA
[Using AA similar condition]
‚ąī ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†¬†![]()
[‚ąĶ ¬†Corresponding sides of two similar triangles are proportional]
⇒    AC2 = BC × DC.
(iii) In right triangle ADB and ‚ąÜCDA,
‚ą†DAB = ‚ą†DCA = 90¬į
‚ą†BDA = ‚ą†ADC (common)
‚ąī ¬†¬†¬†‚ąÜADB ~ ‚ąÜCDA
[Using AA similar condition]
‚ąī ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬† ¬†¬†![]()
[‚ąĶ Corresponding sides of two similar triangles are proportional]
⇒    AD2 = BD × CD.
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type