 Short Answer Type
Short Answer TypeSides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio
(a) 2 : 3 (b) 4 : 9
(c) 81 : 16 (d) 16 : 81.
 Long Answer Type
Long Answer TypeIn the given fig, ABD is a triangle right angled at A and AC ⊥ BD. Show that
(i) AB2 = BC .BD
(ii) AC2 = BC. DC
(iii) AD2 = BD . CD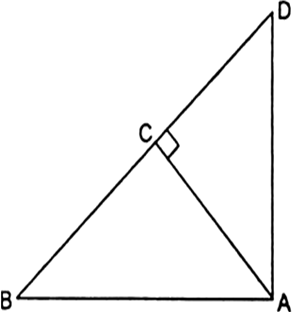
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type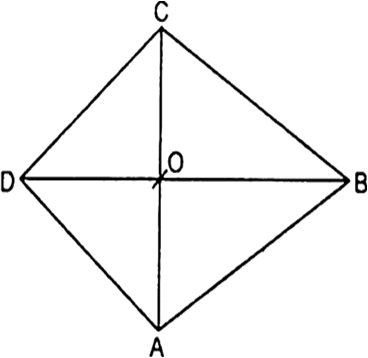
Given: ABCD is a Rhombus in which AC and BD are diagonals which intersect each other at O.
To Prove : AB2 + BC2 + CD2 + DA2 = AC2 + BD2
Proof : We know that diagonals of rhombus bisect each other at right angle.
Therefore,
∠AOB=∠BOC = ∠COD = ∠DOA = 90°
Now, in right angle ∆AOB
AB2 = OA2 + OB2 ...(i)
[Using Pythagoras theorem]
In, ∆BOC right triangle we have
BC2 = OB2 + OC2 ...(ii)
[Using Pythagoras theorem]
In, ∆COD right triangle we have
CD2 = OC2 + OD2 ...(iii)
[Using Pythagoras theorem]
In, ∆AOD right triangle we have
AD2 = OD2 + OA2 ...(iv)
[Using Pythagoras theorem]
Adding (i), (ii), (iii) and (iv), we get
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Hence, ![]()
