Two poles of heights 6 m and 11 m stand on a plane ground. If t
    • Zigya Logo

    Previous Year Papers

    Download Solved Question Papers Free for Offline Practice and view Solutions Online.

    Test Series

    Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

    Test Yourself

    Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.
    Advertisement

    Triangles

    Multiple Choice QuestionsLong Answer Type

    221. In the given Fig, O is a point in the interior of a triangle ABC, OD ⊥ BC,OE ⊥ AC and OF ⊥ AB. Show that
    (i) OA2 + OB2 + OC2 - OD2 - OE2 - OF2 = AF2 + BD2 + CE2,
    (ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2.
    1753 Views
    Answer

    Multiple Choice QuestionsShort Answer Type

    222.

    A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.

    139 Views
    Answer
    223. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
    136 Views
    Answer

    Multiple Choice QuestionsLong Answer Type

    224. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after 1 1 half hours ?
    132 Views
    Answer
    Advertisement
    Advertisement
    Zigya App

    225.

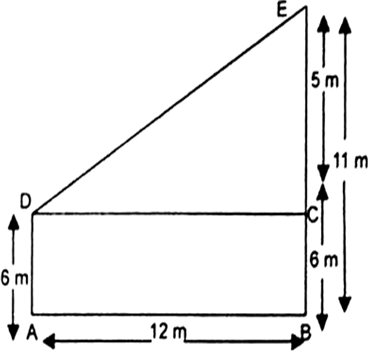
    Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.

    Given: AD and BE are two poles of height 6 cm and 11 m respectively. D and E are their tops respectively. A and B are their feet respectively such that AB = 12 m.
    Given: AD and BE are two poles of height 6 cm and 11 m respectively.

    Required : To find out DE.
    Construction: Draw DC ⊥ BE. Join DE.
    Determination: ABCD is a rectangle and BC and AD are its opposite sides.
    ∴    BC = AD
    [∵ Opposite sides of a rectangle are equal]   = 6 m
    Similarly,    DC = AB = 12 cm
    Now,    CE = BE - BC
    = 11 m - 6 m = 5 m
    Again, in right triangle DCE,
    DE2 = DC2 + CE2
    [By Pythagoras theorem]
    = (12)2 + (5)2
    = 144 + 25 = 169
    rightwards double arrow space space space space space space space space space space space space space space DE equals square root of 169 space equals space 13 space cm
    Hence, the distance between their tops is 13 m.
    156 Views
  • Switch Icon Switch
    • Advertisement

    Multiple Choice QuestionsShort Answer Type

    226. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2.
    1006 Views
    Answer

    Multiple Choice QuestionsLong Answer Type

    227. The perpendicular from A on side BC of a ∆ABC intersects BC at D such that DB = 3 CD. Prove that 2AB2 = 2AC2 +BC2.
    1138 Views
    Answer
    228. In an equilateral ABC, D is a point on side BC such that BD equals 1 third BC. Prove that 9AD2 = 7AB2. 
    1843 Views
    Answer
    Advertisement
    229. In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
    352 Views
    Answer

    Multiple Choice QuestionsShort Answer Type

    230. Tick the correct answer and justify: In ∆ABC, AB equals 6 square root of 3 space cm comma space AC space equals space 12 space cm space and space BC space equals space 6 space cm. The angle B is:
    (A) 120°                (B) 60°
    (C) 90°                  (D) 45°
    226 Views
    Answer
    Advertisement
    Flag Popup Icon
    Flag it
    Submit
    Flag Popup Icon
    Switch to
    flexipad
    Share It Icon
    Share it
    Share It
    Share it