Long Answer Type
Long Answer TypeIn the given fig., D is a point on hypotenuse AC of ∆ABC, DIM ⊥ BC and DN ⊥ AB.
Prove that:
(i) DM2 = DN × MC.
(ii) DN2 = DM × AN.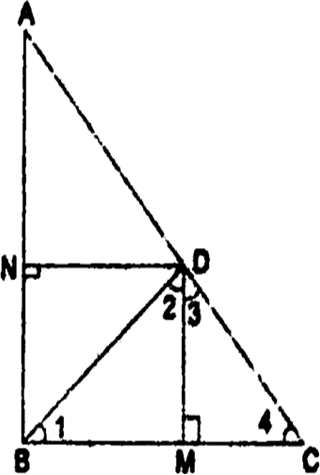
We have,
AB ⊥ BC and DM ⊥ BC
⇒ AB || DM
Similarly, we have
CB ⊥ AB and DN ⊥ AB
⇒ CB || DN
Hence, quadrilateral BMDN is a rectangle.
∴ BM = ND
(i) In ∆BMD, we have
∠1 + ∠BMD + ∠2 = 180°
⇒ ∠1 + 90° + ∠2 = 180°
⇒ ∠1 + ∠2 = 90°
Similarly, in ∆DMC, we have
∠3 + ∠4 = 90°
Since BD ⊥ AC. Therefore
∠2 + ∠3 = 90°
Now, ∠1 + ∠2 = 90°and ∠2 + ∠3 = 90°
⇒ ∠1 + ∠2 = ∠2 + ∠3
⇒ ∠1 = ∠3
Also, ∠3 + ∠4 = 90° and ∠2 + ∠3 = 90°
⇒ ∠3 + ∠4 = ∠2 + ∠3 ⇒ ∠2 = ∠4
Thus, in ∆'s BMD and DMC, we have
∠1 = ∠3 and ∠2 = ∠4
Therefore, by using AA similar condition
![]()
![]()
![]()
![]()
![]()
![]()
(ii) Proceeding as in (i), we can prove that
![]()
 Short Answer Type
Short Answer TypeIn the given fig., ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2 BC . BD.
In the given Fig, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2= AB2 + BC2 - 2 BC.BD.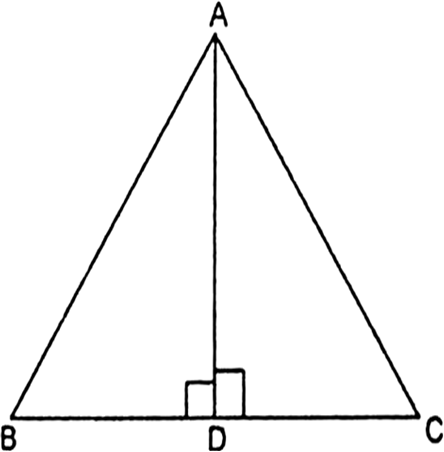
 Long Answer Type
Long Answer TypeIn the given fig, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
(i) ![]()
(ii) ![]()
(iii) ![]()
In the given fig, two chords AB and CD intersect each other at the point P. Prove that:
(i) ∆APC ~ ∆DPB.
(ii) AP . PB = CP . DP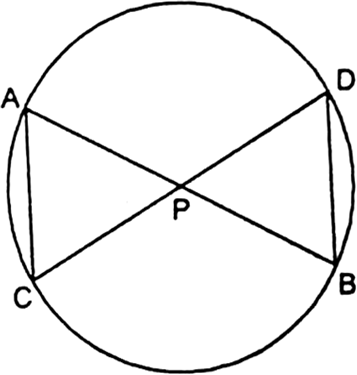
In the given Fig, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ∆PAC ~ ∆PDB.
(ii) PA. PB = PC . PD.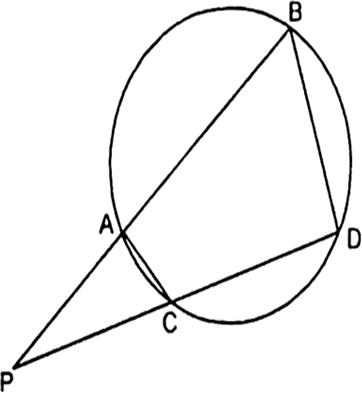
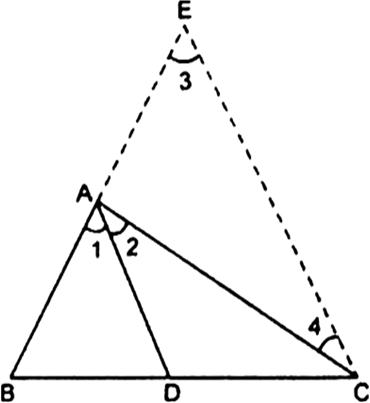
In the given fig, D is a point on side BC of ∆ABC such that ![]() Prove that AD is the bisector of ∠BAC.
Prove that AD is the bisector of ∠BAC.