Long Answer Type
Long Answer TypeIn the given fig., D is a point on hypotenuse AC of ∆ABC, DIM ⊥ BC and DN ⊥ AB.
Prove that:
(i) DM2 = DN × MC.
(ii) DN2 = DM × AN.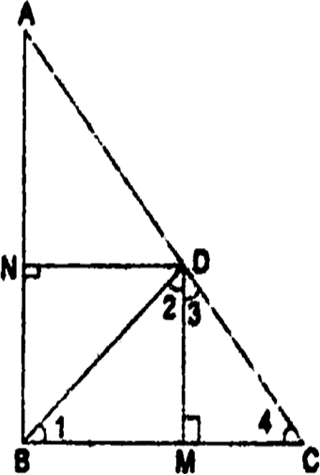
 Short Answer Type
Short Answer TypeIn the given fig., ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2 BC . BD.
Given: An obtuse triangle ABC, obtuse angled at B, and AD ⊥ CB produced.
To Prove : AC2 = AB2 + BC2 + 2BC.BD
Proof: In right triangle ADB, we have
AB2 = AD2 + BD2 ...(i)
[Using Pythagoras theorem]
In ∆ADC, we have
AC2 = AD2 + DC2
⇒ AC2 = AD2 + (DB + BC)2
⇒ AC2 = AD2 + DB2 + BC2 + 2DB.BC
⇒ AC2 = AB2 + BC2 + 2BC.BD
[from (i), we have AB2 = AD2 + BD2]
In the given Fig, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2= AB2 + BC2 - 2 BC.BD.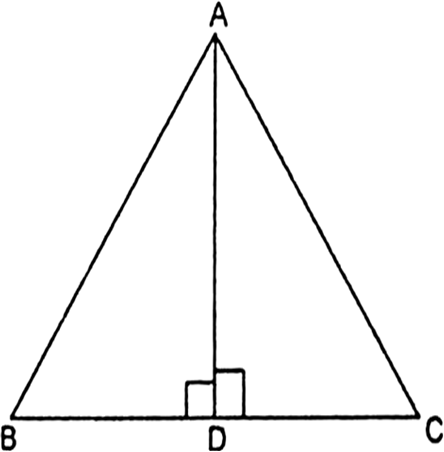
 Long Answer Type
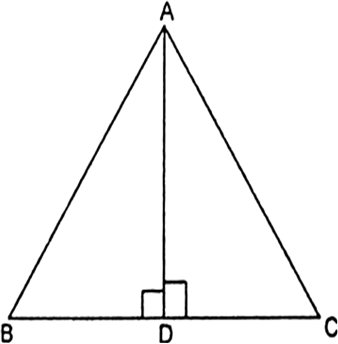
Long Answer TypeIn the given fig, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
(i) ![]()
(ii) ![]()
(iii) ![]()
In the given fig, two chords AB and CD intersect each other at the point P. Prove that:
(i) ∆APC ~ ∆DPB.
(ii) AP . PB = CP . DP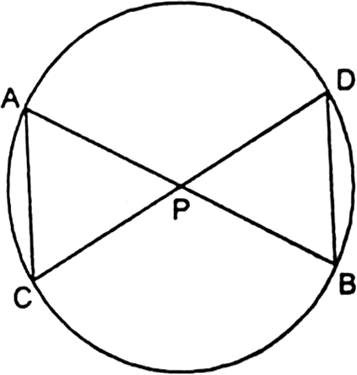
In the given Fig, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ∆PAC ~ ∆PDB.
(ii) PA. PB = PC . PD.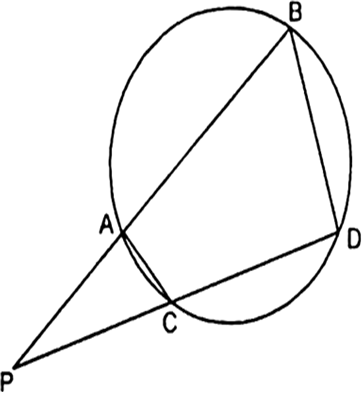
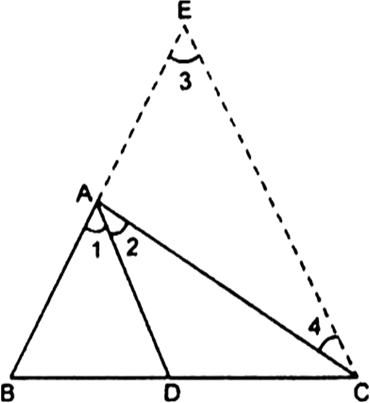
In the given fig, D is a point on side BC of ∆ABC such that ![]() Prove that AD is the bisector of ∠BAC.
Prove that AD is the bisector of ∠BAC.