Long Answer Type
Long Answer TypeIn the given fig., D is a point on hypotenuse AC of ∆ABC, DIM ⊥ BC and DN ⊥ AB.
Prove that:
(i) DM2 = DN × MC.
(ii) DN2 = DM × AN.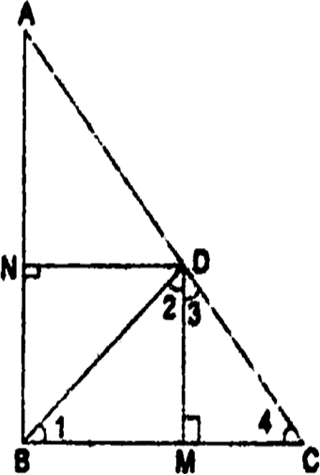
 Short Answer Type
Short Answer TypeIn the given fig., ABC is a triangle in which ∠ABC > 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2 BC . BD.
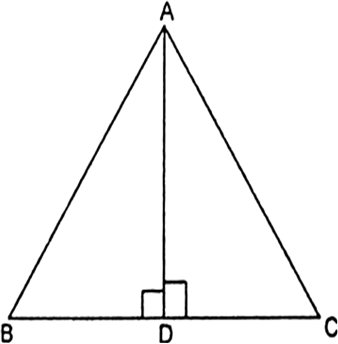
In the given Fig, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2= AB2 + BC2 - 2 BC.BD.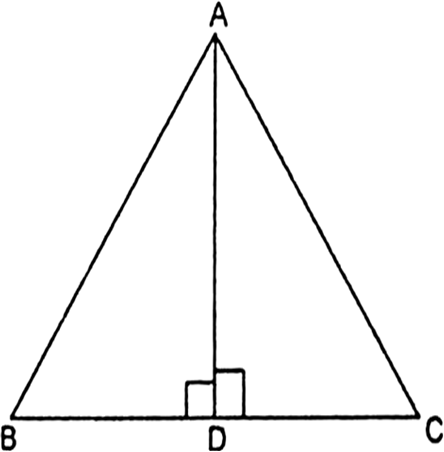
 Long Answer Type
Long Answer TypeIn the given fig, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:
(i) ![]()
(ii) ![]()
(iii) ![]()
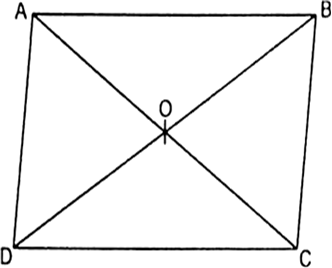
Given: ABCD is a parallelogram in which AC and BD are diagonals which intersect each other at O.
To Prove: AB2 + BC2 + CD2 + DA2 = AC2 + BD2
Proof: Since diagonals of parallelogram bisect each other.
Therefore, BO and DO are medians of ∆ABC and ∆ADC, respectively.
We know that the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median which bisects the third side.
Now, in ∆ABC,
∵ OB is a median

In the given fig, two chords AB and CD intersect each other at the point P. Prove that:
(i) ∆APC ~ ∆DPB.
(ii) AP . PB = CP . DP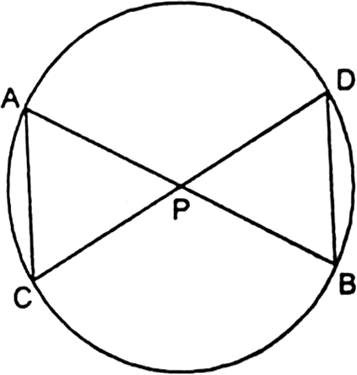
In the given Fig, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ∆PAC ~ ∆PDB.
(ii) PA. PB = PC . PD.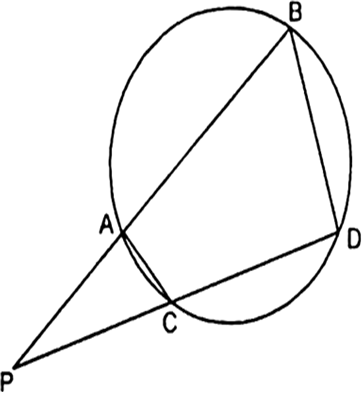
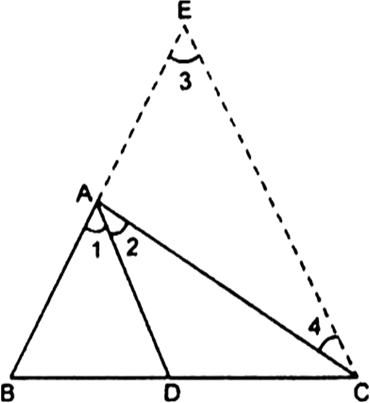
In the given fig, D is a point on side BC of ∆ABC such that ![]() Prove that AD is the bisector of ∠BAC.
Prove that AD is the bisector of ∠BAC.