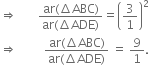Long Answer Type
Long Answer TypeIn the given Fig, two triangles ABC and DBC lie on the same side of base BC. P is a point on BC such that PQ || BA and PR || BD. Prove that: QR || AD. 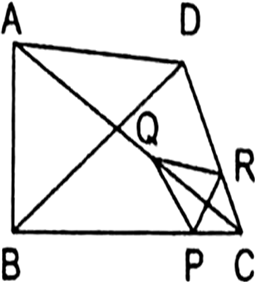
 Short Answer Type
Short Answer TypeIn the given fig, ST || QR, PS = 2 cm and SQ = 3 cm. What is the ratio of the area of ∆PQR to the area of ∆PST?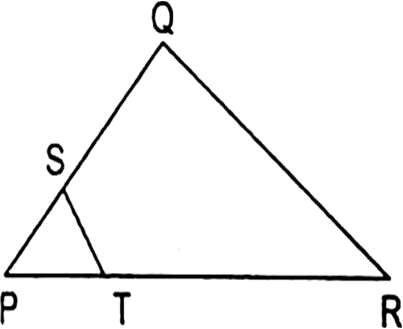
In the given Fig. PB and QA are perpendiculars to segment AB. If PO = 5 cm, QO = 7 cm and area ∆POB = 150 cm2 find the area of ∆QOA.
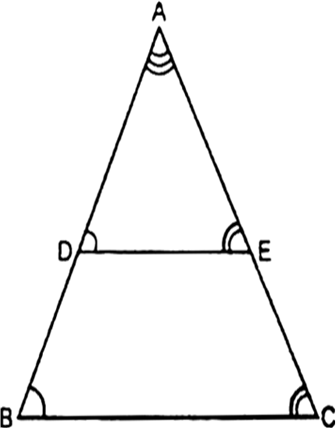
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeIn the given fig, DE is parallel to BC and AD = 1 cm, BD = 2 cm. What is the ratio of the area of ∆ABC to the area of ∆ADE?
It is given that AD = 1 cm, BD = 2 cm and DE || BC
In ∆ADE and ∆ABC,
∠ADE = ∠ABC (Corresponding angles)
∠A = ∠A [Common]
Therefore, by A.A. similar condition
∆ADE ~ ∆ABC
Ratio of areas of similar triangles is equal to the square of the ratio of the corresponding sides.
∴ ![]()