Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

261. D, E and F are the mid points of the sides AB, BC and CA respectively ∆ABC. Find

<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

351 Views

262.

In the given fig, P and Q are points on the sides AB and AC respectively of $increment ABC$ such that AP = 3.5 cm, PB = 7 cm, AQ = 3 cm and QC = 6 cm. If PQ = 4.5 cm, find BC.

994 Views

263.
In the given Fig, PQ = 24 cm, QR = 26 cm, ∠PAR = 90°, PA = 6 cm, and AR = 8, cm. Find ∠QPR.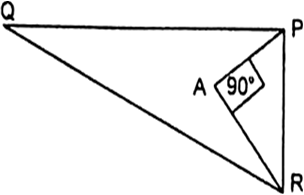

In right triangle APR, we have
AP = 6cm., AR = 8 cm., And, ∠A = 90°
∴ By using Converse of Pythagoras Theorem, We have
PR² = AR² + AP²⇒ PR² = 8² + 6²= 64 + 36 = 100
PR = 10 cm.
Now, in triangle PQR, we have
PQ = 24 cm., QR = 26 cm. and, PR = 10 cm.
Here, we have,
PQ² + PR² = (24)² + (10)²= 576 + 100 = 676 = QR²Hence,
By Converse of Phythagoras Theorem ∠QPR = 90°

3264 Views

264. ∆ABC and ∆DBC lie on the same side of base BC. From a point P on base BC, PQ || AB and PR || BD are drawn. Prove that QR || AD.

115 Views

265. If D and E are the points on the sides AB and AC of a triangle ABC respectively, such that AD = 6 cm, BD = 9 cm, AE = 8 cm and EC = 12 cm. Show that DE is parallel to BC.

101 Views

266. The figure drawn along side, shows a ∆ABC, in which DE is parallel to BC. If

<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array) #1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493) #2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs() #3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...') #4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array) #5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array) #6 {main}</pre>

and AC = 7.2 cm; find AE.

281 Views

267. The given figure shows a quadrilateral ABCD in which AB is parallel to DC, OA = 3x - 19, OB = x - 3, OC = x - 5 and OD = 3. Find the value of x.

94 Views

Long Answer Type

268. If the bisector of an angle of a triangle bisects the opposite side, prove that triangle is isosceles.

236 Views

269. ABC and DBC are two right triangles with common hypotenuse BC and with their sides AC and BD intersecting at point P. Prove AP × PC = DP × pb.

105 Views

Short Answer Type

270. In the given figure, AB || CD, AB = 12 cm, OB = (3x + 3) cm, CD = 5.v cm and OC = (6x + 1) cm. Find the value of x.

86 Views

Previous Year Papers

Test Series

Test Yourself

Short Answer Type

263. In the given Fig, PQ = 24 cm, QR = 26 cm, ∠PAR = 90°, PA = 6 cm, and AR = 8, cm. Find ∠QPR.

Long Answer Type

Short Answer Type

263.
In the given Fig, PQ = 24 cm, QR = 26 cm, ∠PAR = 90°, PA = 6 cm, and AR = 8, cm. Find ∠QPR.