 Long Answer Type
Long Answer Type
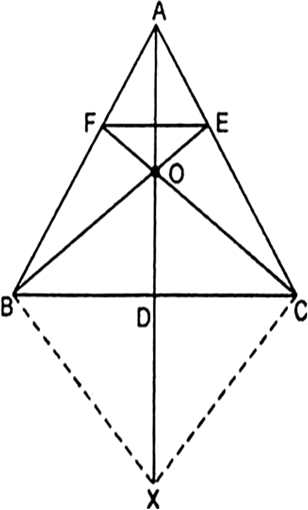
(ii) FE || BC
Const : Join B-X and C-X
Proof: We have,
BD = CD
and OD = DX
⇒ BC and OX bisect each other.
⇒ OBXC is a parallelogram
⇒ BX || CO and CX || BO
⇒ BX || CF and CX || BE
⇒ BX || OF and CX || OE
Now in ∆ABX, we have
OF || BX
Therefore, By using Basic proportionality theorem, we have![]() ...(i)
...(i)
In ∆ACX, we have
OE || CX
Therefore, by using Basic proportionality theorem, we have![]() ...(ii)
...(ii)
Comparing (i) and (ii), we get![]()
Therefore, by using converse of Basic proportionality theorem FE || BC.
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type