Long Answer Type
Long Answer Type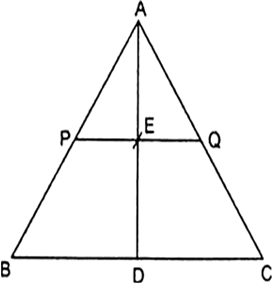
Given: ŌłåABC in which P and Q are points on sides AB and AC respectively such that PQ || BC and AD is a median.
To Prove : AD bisects PQ.
Proof: In ŌłåAPE and ŌłåABD
ŌłĀAPE = ŌłĀABD
[corresponding angles]
and ┬Ā┬Ā┬ĀŌłĀPAE = ŌłĀBAD [common]
Therefore, by using AA similar condition
┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā![]()
![]() ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā
┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā![]() ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā...(i)
┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā...(i)
Now, In ŌłåAQE and ŌłåACD
ŌłĀAQE = ŌłĀACD
[corresponding angles]
ŌłĀQAE = ŌłĀCAD [common]
Therefore, by using A.A. condition
┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā┬Ā![]()
![]()
Comparing (i) and (ii), we have
┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā┬Ā![]()
But ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā![]()
┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā[ŌłĄ ┬ĀAD is a median]![]() ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā
┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā ┬Ā![]()
Hence AD bisects PQ.
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeIn the given Fig.┬ĀDEFG is a square and ŌłĀBAC = 90┬░. Prove that
(i) ŌłåAGF ~ ŌłåDBG.
(ii) ŌłåAGF ~ ŌłåEFC.
(iii) ŌłåDBG ~ ŌłåAEFC
(iv) DE2┬Ā= BD ├Ś EC.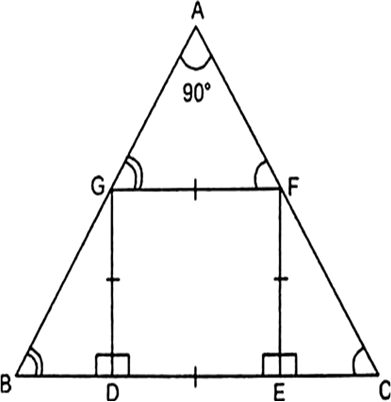
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type