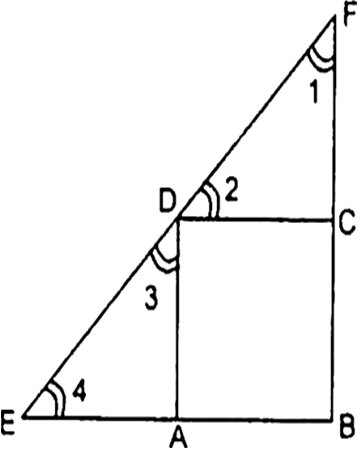
Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeIn the given Fig. DEFG is a square and ∠BAC = 90°. Prove that
(i) ∆AGF ~ ∆DBG.
(ii) ∆AGF ~ ∆EFC.
(iii) ∆DBG ~ ∆AEFC
(iv) DE2 = BD × EC.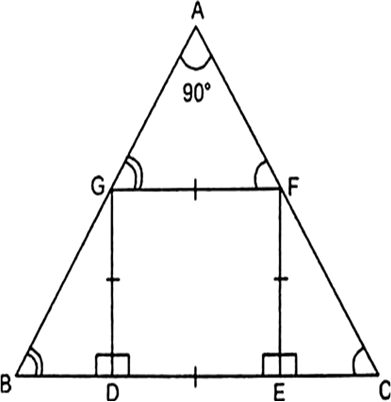
(i) In ∆AGF and ∆DBG
∠A = ∠BDG = 90°
and ∠AGF = ∠DBG
[corresponding angles]
Therefore, by using AA similar condition
∆AGF ~ ∆DBG.
(ii) In ∆AGF and ∆EFC
∠AFG = ∠ECF
[corresponding angles]
and ∠FAG = ∠CEF = 90°
Therefore, by using A.A similar condition
∆AGF ~ ∆EFC
From (i), we have
∆AGF ~ ∆DBG
From (ii), we have
![]()
![]()
![]()
![]()
![]()
[corresponding sides of two similar triangles are proportional]![]()
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type