Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeIn the given Fig. DEFG is a square and ∠BAC = 90°. Prove that
(i) ∆AGF ~ ∆DBG.
(ii) ∆AGF ~ ∆EFC.
(iii) ∆DBG ~ ∆AEFC
(iv) DE2 = BD × EC.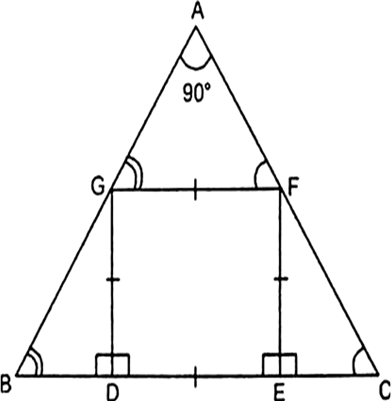
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeIn the given Fig., AC ⊥ BC, BD ⊥ BC and DE ⊥ AB. Prove that ABC ~ BDE.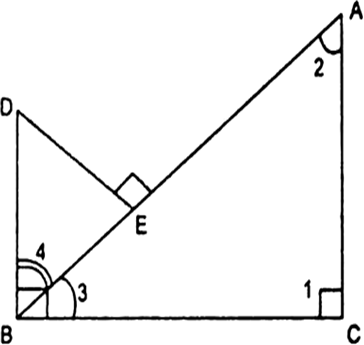
Given: AC ⊥ BC, BD ⊥ BC and DE ⊥ AB.
To Prove : ∆ABC ~ ∆BDE
Proof: ∵ ∠1 = 90° [given]
⇒ ∠2 + ∠3 = 90° ...(i)
and ∠3 + ∠4 = 90° ...(i) [given]
Comparing (i) and (ii), we get
⇒ ∠2 + ∠3 = ∠3 + ∠4
⇒ ∠2 = ∠4
or ∠BAC = ∠DBE
Now, in ∆ABC and ∆BDE
∠BAC = ∠DBE [alternate angles]
and ∠ACB = ∠BED = 90°
Therefore, by using AA similar condition
∆ABC ~ ∆BDE.
 Long Answer Type
Long Answer Type