Long Answer Type
Long Answer TypeIn the given Fig, M is the mid-point of side CD of a parallelogram ABCD. The line BM is drawn intersecting AC at L and AD produced at E. Prove that EL = 2 BL. 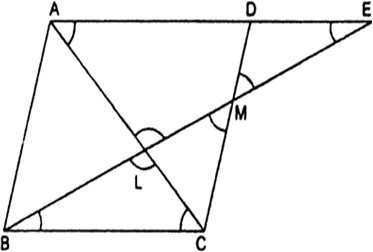
 Short Answer Type
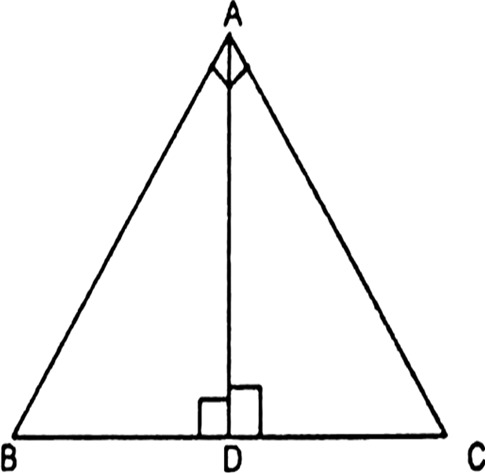
Short Answer TypeIn the given Fig., ∆ABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE, and hence find the lengths of AE and DE.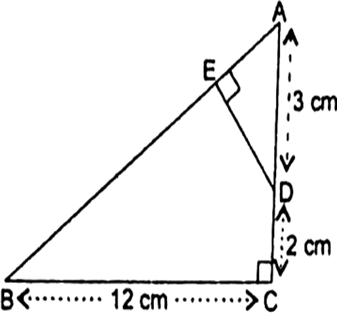
 Long Answer Type
Long Answer Type
In the given Fig, ![]() if the area of XYZ is 32 cm2, then find the area of the quadrilateral PYZQ.
if the area of XYZ is 32 cm2, then find the area of the quadrilateral PYZQ.
We have, ![]()
![]()
[Using converse of Basic proportionality theorem]
Now, in ∆XPQ and ∆XYZ,
∴ ∠XPQ = ∠XYZ [Corresponding angles]
∠X = ∠Y [Common]
Therefore, by using AA similar condition, we have ∆XPQ ~ ∆XYZ![]()
[∵ The ratio of the areas of two similar triangles is equal to the ratio of their corresponding sides]