 Long Answer Type
Long Answer Type
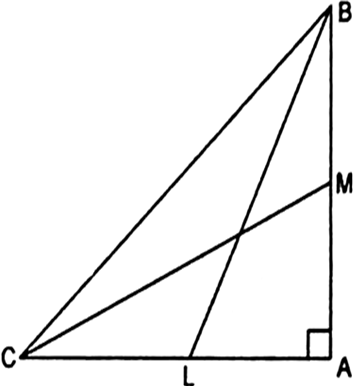
In the given Fig, ABC is a right triangle, right angled at B. AD and CE are two medians drawn from A and C respectively. If AC = 5 cm and ![]() find the length of CE.
find the length of CE.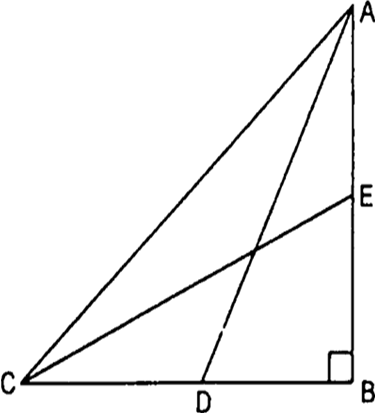
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type

To prove:
AQ2 + BP2 = AB2 + PQ2
Proof: In right ∆ACQ, we have
AQ2 = AC2 + CQ2 ...(i)
[Using Pythagoras theorem]
In right ∆PCB, we have
BP2 = PC2 + BC2 ...(ii)
[Using Pythagoras theorem]
Adding (i) and (ii), we get
AQ2 + BP2 = (AC2 + BC2) + (PC2 + CQ2)
⇒ AQ2 + BP2 = AB2 + PQ2 Proved.
