Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Long Answer Type

331.

In the given Fig. if AD ⊥ BC and $space BD over DA equals DA over DC.$ Prove that ∆ABC is a right triangle.

108 Views

Short Answer Type

332.
In the given Fig., AD ⊥ BC. Prove that AB² + CD² = BD² + AC².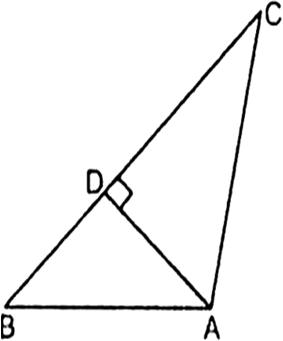

In right ∆ADC. by Pythagoras Theorem,
AC² = AD² + CD² ...(i)
In right ∆ADB, by Pythagoras Theorem,
AB² = AD² + BD² ...(ii)
Subtracting (i) from (ii), we get
AB² - AC² = BD² - CD²⇒ AB² + CD²= BD² + AC² Hence Proved.

188 Views

333. Triangle ABC is right-angled at B and D is the mid-point of BC. Prove that AC² = 4AD² - 3AB².

3897 Views

334. In rhombus ABCD, prove that 4AB² = AC² + BD².

3939 Views

335.

In the given Fig., DE || BC, if $AD over DB equals 3 over 2$ and AE = 4.8 cm, find EC.

88 Views

Long Answer Type

336. In the given figure, PQ || BC. If
(i)

AP over PB equals 2 over 3 space and space AC space equals space 16 space cm comma space space space find space QC.

(ii)

AQ over CQ equals 3 over 5 space and space PB space equals space 7.5 space cm comma space find space AB.

92 Views

337. If three or more parallel lines are intersected by two transversals. Prove that the intercepts made by them on the transversals are proportional.

253 Views

Short Answer Type

338. In quadrilateral ABCD, P is any point in side BC. PQ || AB and PR || BD. Show that QR is parallel to AD.

84 Views

339. If D and E are respectively, the points on the sides AB and AC of a triangle ABC, such that AD = 6 cm, BD = 9 cm, AE = 8 cm and EC = 12 cm then show that DE || BC.

87 Views