Short Answer Type
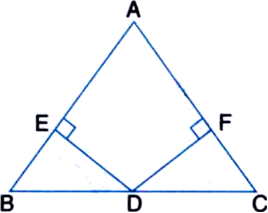
Short Answer TypeGiven: In ∆ABC, D is the mid point of BC. The perpendiculars from D to AB and AC are equal.
To Prove: ∆ABC is isosceles.
Proof: In right triangles DEC and DFB,
Hyp. DC = Hyp. DB
| ∵ D is the mid point of BC
Side DE = Side DF | Given
∴ ∆DEC ≅ ∆DFB
| RHS congruence rule
∴ ∠DCE = ∠DBF
⇒ ∠BCA = ∠CBA
∴ AB = AC
| Sides opposite to equal angles of a triangle are equal
 Long Answer Type
Long Answer Type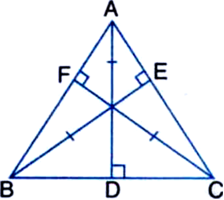
 Short Answer Type
Short Answer Type