Given: In ∆’s ABC and PQR, AB = PQ, AC = PR and altitude AM and altitude PN are equal.
To Prove: ∆ABC ≅ ∆PQR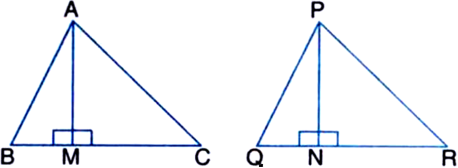

Proof: In right triangles ∠AMB and ∠PNQ,
Hyp. AB = Hyp. PQ    | Given
Side AM = Side PN    | Given
∴ ∆AMB ≅ ∆PNQ
| RHS congruence rule
∴ ∠BAM = ∠QPN    ...(1) | CPCT
In right triangles CAM and RPN,
Hyp. AC = Hyp. PR    | Given
Side AM = Side PN    | Given
∴ ∆CAM ≅ ∆RPN
| RHS congruence rule
∴ ∠CAM = ∠RPN    ...(2) | CPCT
Adding (1) and (2), we get,
∠BAM + ∠CAM = ∠QPN + ∠RPN
⇒ ∠BAC = ∠QPR    ...(3)
In ∆ABC and ∆PQR,
AB = PQ    | Given
BC = QR    | Given
∠BAC = ∠QPR    | From (3)
∴ ∆ABC ≅ ∆PQR
| SAS congruence rule