Short Answer Type
Short Answer Type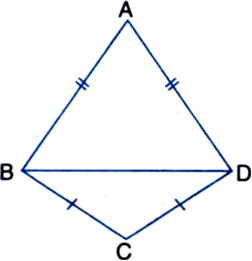
 Long Answer Type
Long Answer Type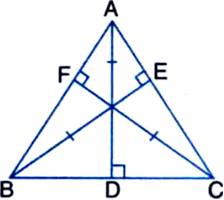
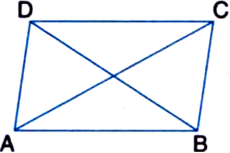
AD = BC
| Opposite sides of a parallelogram are equal
AB = BA | Common
DB = CA | Given
∴ ∆ADB ≅ ∆BCA
| SSS congruence rule
∴ DAB = ∠CBA ...(1) | CPCT
But AD || BC
| Opposite sides of parallelogram ABCD and a transversal AB intersects then
∴ ∠DAB + ∠CBA = 180°
| Sum of consecutive interior angles on the same side of a transversal is 180°
⇒ ∠CBA + ∠CBA = 180° | From (1)
⇒ 2∠CB A = 180°
⇒ ∠CBA = 90°
⇒ ∠ABC = 90°
 Short Answer Type
Short Answer Type