Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

501. In figure, AB > AC, BO and CO are the bisectors of ∠B and ∠C respectively. Show that OB > OC.

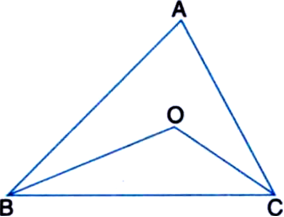
Given: AB > AC, BO and CO are the bisectors of ∠B and ∠C respectively.
To Prove: OB > OC
Proof: ∵ AB > AC | Given
∴ ∠ACB > ∠ABC
| Angle opposite to longer side is greater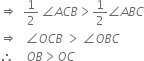

$rightwards double arrow space space 1 half space angle A C B greater than 1 half angle A B C rightwards double arrow space space space angle O C B space greater than space angle O B C therefore space space space space O B greater than O C$

| Side opposite to greater angle is longer