502.

In the given figure, ∠ABD = 130° and ∠EAC = 120°. Prove that AB >  AC.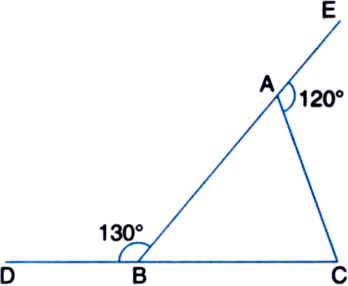

∠ABD + ∠ABC = 180° | Linear Pair Axioms
⇒ 130° + ∠ABC = 180°
⇒    ∠ABC = 50°    ...(1)
∠C AE + ∠C AB = 180° | Linear Pair Axiom
⇒ 120° + ∠CAB = 180°
⇒    ∠CAB = 60°    ...(2)
In ∆ABC,
∠ABC + ∠BCA + ∠CAB = 180°
| Angle sum property of a triangle
⇒ 50° + ∠BCA + 60° = 180°
⇒    ∠BCA = 70°    ...(3)
From (1) and (3),
∠BCA >  ∠ABC
∴ AB >  AC
| Side opposite to greater angle is longer