Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

501. In figure, AB > AC, BO and CO are the bisectors of ∠B and ∠C respectively. Show that OB > OC.

1077 Views

502.

In the given figure, ∠ABD = 130° and ∠EAC = 120°. Prove that AB > AC.

315 Views

503. If AD is the bisector of ∠A of ∆ ABC, show that AB > DB.

111 Views

Long Answer Type

504. 0 is a point in the interior of ∆PQR.

OP + OQ + OR >

1 half

(PQ + QR + RP).

1543 Views

Short Answer Type

505. In figure, D is any point on the base BC produced of an isosceles triangle ∆ABC. Prove that AD > AB.

1992 Views

506. In figure, S is any point in its interior of ∆PQR. Show that SQ + SR < PQ + PR.

Given: S is any point in its interior of ∆PQR.
To Prove: SQ + SR < PQ + PR
Construction: Produce QS to meet PR in T
Proof: In ∆PQT,
PQ + PT > QT
∵ The sum of the lengths of any two sides of a triangle is greater than the length of the third side ...(1)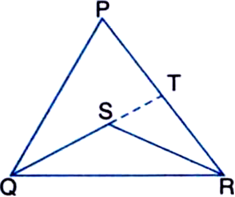

⇒ PQ + PT > QS + ST    ...(2)
| ∵ QT = QS + ST
In ∆SRT,
TR + ST > SR    ...(3)
| ∵ The sum of the lengths of any two sides of a triangle is greater than the length of the third side
Adding (2) and (3), we get
PQ + PT + TR + ST > QS + ST + SR
⇒ PQ + PR + ST > QS + ST + SR
⇒    PQ + PR > SQ + SR
⇒ SQ + SR < PQ + PR

3493 Views