 Short Answer Type
Short Answer Type

(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

Given: AD and BC are equal perpendiculars to a line segment AB.
To Prove: CD bisects AB.
Proof: In ∆O AD and ∆OBC
AD = BC | Given
∠OAD = ∠OBC | Each = 90°
∠AOD = ∠BOC
| Vertically Opposite Angles
∴ ∠OAD ≅ ∆OBC | AAS Rule
∴ OA = OB | C.P.C.T.
∴ CD bisects AB.

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.
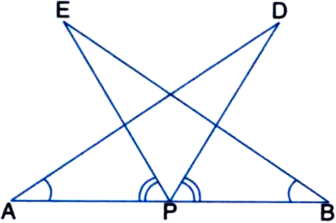
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.
 Long Answer Type
Long Answer Type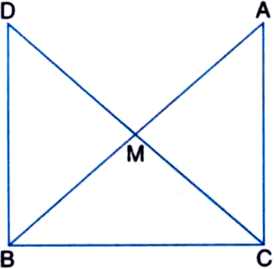
(i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∆DBC ≅ ∆ACB![]()
 Short Answer Type
Short Answer Type
