 Short Answer Type
Short Answer Type

(i) ‚ąÜABD ‚ČÖ ‚ąÜBAC
(ii) BD = AC
(iii) ‚ą†ABD = ‚ą†BAC.


Given: I and m are two parallel lines intersected by another pair of parallel lines p and q.
To Prove: ‚ąÜABC ‚ČÖ ‚ąÜCDA.
Proof: ‚ąĶ AB || DC
and    AD || BC
‚ąī Quadrilateral ABCD is a parallelogram.
| ‚ąĶ A quadrilateral is a parallelogram if both the pairs of opposite sides are parallel
‚ąī BC = AD ¬†¬†¬†...(1)
| Opposite sides of a ||gm are equal
AB = CD    ...(2)
| Opposite sides of a ||gm are equal
and ‚ą†ABC = ‚ą†CDA ¬†¬†¬†...(3)
| Opposite angles of a ||gm are equal
In ‚ąÜABC and ‚ąÜCDA,
AB = CD    | From (2)
BC = DA    | From (1)
‚ą†ABC = ‚ą†CDA ¬†¬†¬†| From (3)
‚ąī ‚ąÜABC ‚ČÖ ‚ąÜCDA. ¬†¬†¬†| SAS Rule
Line I is the bisector of an angle ‚ą†A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ‚ą†A (see figure). Show that:
(i) ‚ąÜAPB ‚ČÖ ‚ąÜAQB
(ii) BP = BQ or B is equidistant from the arms of ‚ą†A.
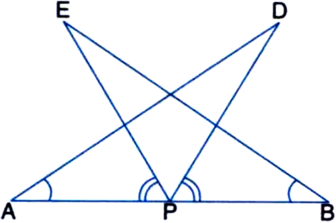
(i) ‚ąÜDAP ‚ČÖ ‚ąÜEBP
(ii) AD = BE.
 Long Answer Type
Long Answer Type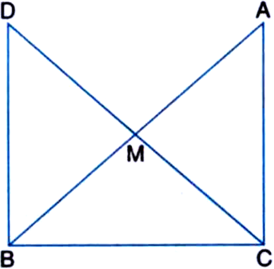
(i) ¬†¬†¬†‚ąÜAMC ‚ČÖ ‚ąÜBMD
(ii) ¬†¬†¬†‚ą†DBC is a right angle
(iii) ¬†¬†¬†‚ąÜDBC ‚ČÖ ‚ąÜACB![]()
 Short Answer Type
Short Answer Type
