Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

1. In quadrilateral ACBD, AC = AD and AB bisects ∠A (see figure). Show that ∆ABC ≅ ∆ABD. What can you say about BC and BD?

3225 Views

2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see figure). Prove that:

(i) ∆ABD ≅ ∆BAC
(ii) BD = AC
(iii) ∠ABD = ∠BAC.

3614 Views

3. AD and BC are equal perpendiculars to a line segment AB (see figure). Show that CD bisects AB.

1639 Views

4. I and m are two parallel lines intersected by another pair of parallel lines p and q (see figure). Show that ∆ABC ≅ ∆CDA.

1471 Views

Line I is the bisector of an angle ∠A and B is any point on I. BP and BQ are perpendiculars from B to the arms of ∠A (see figure). Show that:
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ or B is equidistant from the arms of ∠A.

1288 Views

6. In figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

890 Views

7. AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see figure). Show that.

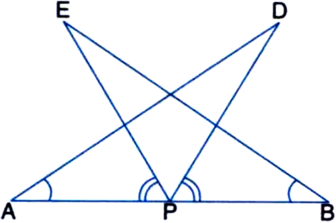
(i) ∆DAP ≅ ∆EBP
(ii) AD = BE.

661 Views

Long Answer Type

8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see figure). Show that:

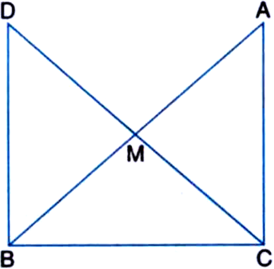
(i)    ∆AMC ≅ ∆BMD
(ii)    ∠DBC is a right angle
(iii)    ∆DBC ≅ ∆ACB
$left parenthesis iv right parenthesis space space space space CM equals 1 half increment ACB$

Given: In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B.

To Prove: (i) ∆AMC ≅ ∆BMD
(ii) ∠DBC is a right angle
(iii) ∠DBC ≅ ∆ACB
$left parenthesis iv right parenthesis space CM equals 1 half AB$

(i) In ∆AMC and ∆BMD,
AM = BM
| ∵ M is the mid-point of the hypotenuse AB
CM = DM    | Given
∠AMC = ∠BMD
| Vertically Opposite Angles
∴ ∆AMC ≅ ∆BMD. | SAS Rule
(ii)    ∵ ∆AMC ≅ ∆BMD
| From (i) above
∠ACM = ∠BDM    | C.P.C.T.
But these are alternate interior angles and they are equal
∴ AC || BD
Now, AC || BD and a transversal BC intersects them
∴ ∠DBC + ∠ACB = 180°
| ∵ The sum of the consecutive interior angles on the same side of a transversal is
180°
⇒ ∠DBC + 90° = 180°
| ∵ ∠ACB = 90° (given)
⇒     ∠DBC = 180° - 90° = 90°
⇒ ∠DBC is a right angle.
(iii)    In ∆DBC and ∆ACB,
∠DBC = ∠ACB (each = 90°)
| Proved in (ii) above
BC = CB    | Common
∵ ∆AMC ≅ ∆BMD    | Proved in (i) above
∴ AC = BD    | C.P.C.T.
∴ ∆DBC ≅ ∆ACB.    | SAS Rule
(iv)    ∵ ∆DBC ≅ ∆ACB
| Proved in (iii) above
∴ DC = AB    | C.P.C.T.

$rightwards double arrow$ 2CM = AB

   $vertical line space because space space DM equals CM equals 1 half DC$
$rightwards double arrow space space space space space CM equals 1 half AB.$