 Short Answer Type
Short Answer Type

(i) вИЖABD вЙЕ вИЖBAC
(ii) BD = AC
(iii) вИ†ABD = вИ†BAC.


Line I is the bisector of an angle вИ†A and B is any point on I. BP and BQ are perpendiculars from B to the arms of вИ†A (see figure). Show that:
(i) вИЖAPB вЙЕ вИЖAQB
(ii) BP = BQ or B is equidistant from the arms of вИ†A.
(i) вИЖDAP вЙЕ вИЖEBP
(ii) AD = BE.
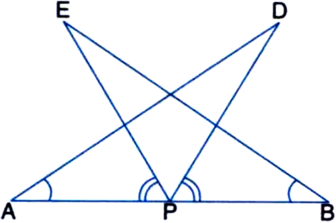
 Long Answer Type
Long Answer Type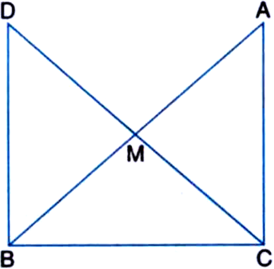
(i) ¬†¬†¬†вИЖAMC вЙЕ вИЖBMD
(ii) ¬†¬†¬†вИ†DBC is a right angle
(iii) ¬†¬†¬†вИЖDBC вЙЕ вИЖACB![]()
 Short Answer Type
Short Answer Type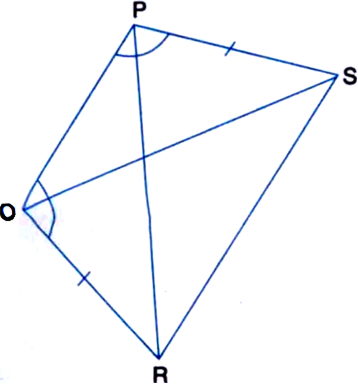
In вИЖQPR and вИЖPQS,
QR = PS    | Given
вИ†RQP = вИ†SPQ ¬†¬†¬†| Given
PQ = PQ    | Common
вИі вИЖQPR вЙЕ вИЖPQS ¬†¬†¬†| SAS Axiom
вИі PR = QS ¬†¬†¬†| C.P.C.T.
and ¬†¬†¬†вИ†QPR = вИ†PQS. ¬†¬†¬†| C.P.C.T.

