Short Answer Type
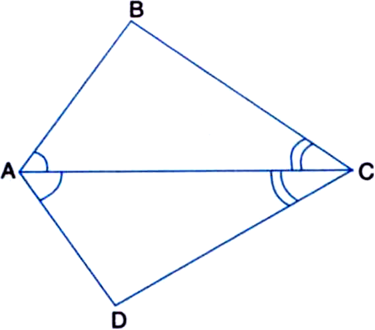
AB is a line-segment. AX and BY are two equal line-segments drawn on opposite sides of line AB such that AX || BY. If AB and XY intersect each other at P. Prove that:
(i)    ∆APX ≅ ∆BPY
(ii) Â Â Â AB and XY bisect each other at P.
Long Answer TypeShort Answer TypeIn figure given below, AD is the median of ∆ABC.
BE ⊥ AD, CF ⊥ AD. Prove that BE = CF.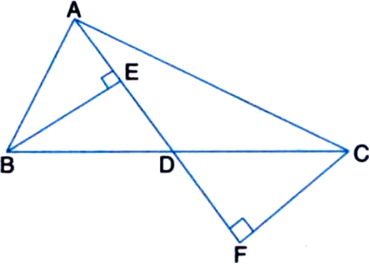
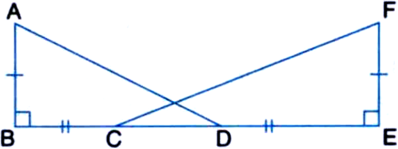
Given:
AB = FE, BC = ED,
AB ⊥ BD and FE ⊥ EC
To Prove: AD = FC
Proof: In ∆ABD and ∆FEC,
AB = FE Â Â Â ...(1) | Given
∠ABD = ∠FEC    ...(2)
| Each = 90°
BC = ED Â Â Â | Given
⇒ BC + CD = ED + DC
⇒    BD = EC    ...(3)
In view of (1), (2) and (3),
∆ABD ≅ ∆FEC
| SAS congruence rule
∴ AD = FC    | CPCT
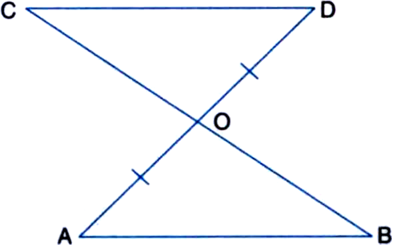
Line-segment AB is parallel to another line-segment CD. O is the mid-point of AD (see figure). Show that: (i) ∆AOB ≅ ∆DOC (ii) O is also the mid-point of BC.
Switch
