Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Triangles

Short Answer Type

31. ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal (see figure). Show that:

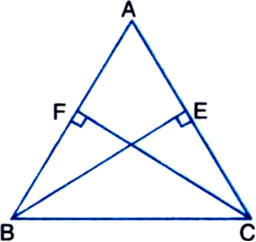
(i) ∆ABE ≅ ∆ACF
(ii) AB = AC, i.e., ∆ABC is an isosceles triangle.

346 Views

32. ABC and DBC are two isosceles triangles on the same base BC (see figure). Show that ∠ABD = ∠ACD.

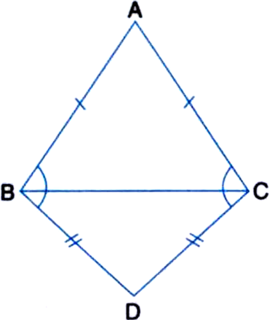
Given: ABC and DBC are two isosceles triangles on the same base BC.
To Prove: ∠ABD = ∠ACD.
Proof: ∵ ABC is an isosceles triangle on the base BC.
∴ ∠BC = ∠ACB    ...(1)
∵ DBC is an isosceles triangle on the base BC
∴ ∠DBC = ∠DCB    ...(2)
Adding the corresponding sides of (1) and (2), we get
∠ABC + ∠DBC = ∠ACB + ∠DCB
⇒    ∠ABD = ∠ACD.

1318 Views

Long Answer Type

33.

∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∆BCD is a right angle.

2598 Views

Short Answer Type

34. ABC is a right angled triangle in which ∠A = 90° and AB = AC. Find ∠B and ∠C.

1262 Views

35. Show that the angles of an equilateral triangle are 60° each.

179 Views

36. Angles A, B and C of a triangle ABC are equal to each other. Prove that ∆ABC is equilateral.

170 Views

37. BD and CE are the bisectors of ∠B and ∠C of an isosceles triangle ABC with AB = AC. Prove that BD = CE.

1965 Views

Long Answer Type

38.

ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that AD bisects ∠BAC and AB = CD. Prove that ∠BAC = 72°.
[Hint. Take a point P on AC such that BP bisects ∠B. Join P and D.]

1214 Views

Short Answer Type

39. Suppose line segments AB and CD intersect at O in such a way that AO = OD and OB = OC. Prove that AC = BD but AC may not be parallel to BD.

2451 Views

40. In the figure, D and E are points on the base BC of a ∆ABC such that AD = AE and ∠BAD = ∠CAE. Prove that AB = AC.

2506 Views