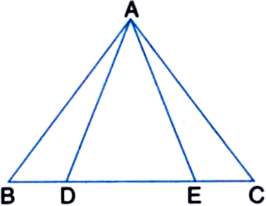
Short Answer Type
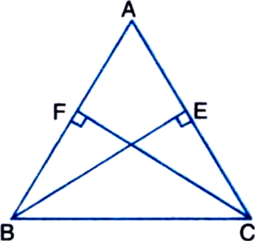
(i) ∆ABE ≅ ∆ACF
(ii) AB = AC, i.e., ∆ABC is an isosceles triangle.
Long Answer Type∆ABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∆BCD is a right angle.
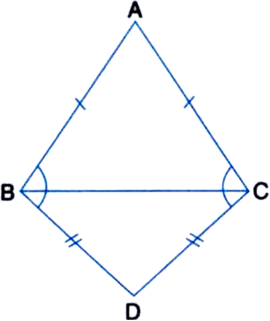
Short Answer Type∵ ∠A = ∠B
∴ BC = CA ...(1)
| Sides opposite to equal angles of ∆ABC
∵ ∠B = ∠C
∴ CA = AB ...(2)
| Sides opposite to equal angles of ∆ABC
∵ ∠C = ∠A
∴ AB = BC ...(3)
| Sides opposite to equal angles of ∆ABC
From (1), (2) and (3), we have
AB = BC = CA
⇒ ∆ABC is equilateral.
Long Answer TypeABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that AD bisects ∠BAC and AB = CD. Prove that ∠BAC = 72°.
[Hint. Take a point P on AC such that BP bisects ∠B. Join P and D.]
Short Answer Type
Switch
