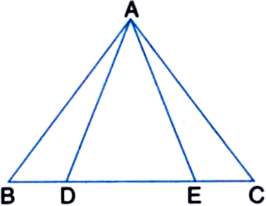
Short Answer Type
Short Answer Type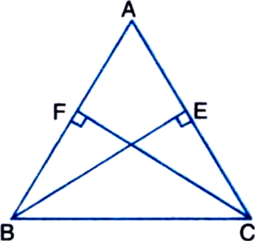
(i) ¬†¬†¬†‚ąÜABE ‚ČÖ ‚ąÜACF
(ii) ¬†¬†¬†AB = AC, i.e., ‚ąÜABC is an isosceles triangle.
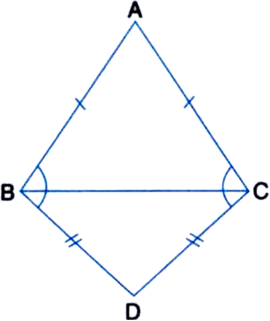
 Long Answer Type
Long Answer Type‚ąÜABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ‚ąÜBCD is a right angle.¬†
 Short Answer Type
Short Answer Type‚ąĶ AB = AC
‚ąī ‚ą†ACB = ‚ą†ABC
| Angles opposite to equal sides of ‚ąÜABC
‚áí ¬†¬†¬†2‚ą†2 = 2‚ą†1
| ‚ąĶ CE and BD are the bisectors of ‚ą†C and ‚ą†B respectively
‚áí ¬†¬†¬†‚ą†2 = ‚ą†1
⇒    BP = PC    ...(1)
| Sides opposite to equal angles of ‚ąÜPBC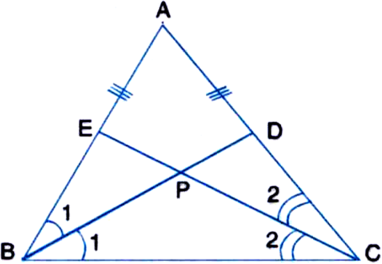
In ‚ąÜBPE and ‚ąÜCPD,
BP = CP    | Proved above
‚ą†EBP = ‚ą†DCP ¬†¬†¬†| Proved above
‚ą†BPE = ‚ą†CPD
| Vertically Opposite Angles
‚ąī ‚ąÜBPE ‚ČÖ ‚ąÜCPD ¬†¬†¬†| ASA Axiom
PE = PD    | C.P.C.T.
⇒    PD = PE    ...(2)
Adding (1) and (2), we get
BP + PD = PC + PE
⇒    BD = CE.
 Long Answer Type
Long Answer TypeABC is a triangle in which ‚ą†B = 2‚ą†C. D is a point on side BC such that AD bisects ‚ą†BAC and AB = CD. Prove that ‚ą†BAC = 72¬į.
[Hint. Take a point P on AC such that BP bisects ‚ą†B. Join P and D.]
 Short Answer Type
Short Answer Type